Find the cooridnates of point A, where AB is a diameter of a circle whose centre is (3,-2) and B is the point (2,4).
To find the coordinates of point A, where AB is a diameter of a circle with center C at (3, -2) and point B at (2, 4), we can follow these steps:
Step 1: Understand the relationship between the center and the endpoints of the diameter
The center of the circle is the midpoint of the diameter AB. Therefore, we can use the midpoint formula to relate the coordinates of points A and B to the center C.
Step 2: Use the midpoint formula
The midpoint M of a line segment with endpoints (x1, y1) and (x2, y2) is given by:
M=(x1+x22,y1+y22)
In our case, the midpoint C (3, -2) is equal to the midpoint of points A (x, y) and B (2, 4).
Step 3: Set up the equations
Using the midpoint formula, we can set up two equations:
1. For the x-coordinates:
3=x+22
2. For the y-coordinates:
−2=y+42
Step 4: Solve the first equation for x
Multiply both sides of the first equation by 2:
6=x+2
Now, subtract 2 from both sides:
x=6−2=4
Step 5: Solve the second equation for y
Multiply both sides of the second equation by 2:
−4=y+4
Now, subtract 4 from both sides:
y=−4−4=−8
Step 6: Write the coordinates of point A
Now that we have found the values of x and y, we can express the coordinates of point A:
A=(4,−8)
Final Answer
The coordinates of point A are (4, -8).
---
The center of the circle is the midpoint of the diameter AB. Therefore, we can use the midpoint formula to relate the coordinates of points A and B to the center C.
The midpoint M of a line segment with endpoints (x1, y1) and (x2, y2) is given by:
M=(x1+x22,y1+y22)
In our case, the midpoint C (3, -2) is equal to the midpoint of points A (x, y) and B (2, 4).
Using the midpoint formula, we can set up two equations:
1. For the x-coordinates:
3=x+22
2. For the y-coordinates:
−2=y+42
Multiply both sides of the first equation by 2:
6=x+2
Now, subtract 2 from both sides:
x=6−2=4
Multiply both sides of the second equation by 2:
−4=y+4
Now, subtract 4 from both sides:
y=−4−4=−8
Now that we have found the values of x and y, we can express the coordinates of point A:
A=(4,−8)
The coordinates of point A are (4, -8).
Topper's Solved these Questions
- SAMPLE PAPER (SELF ASSESSMENT) 12BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER (SELF ASSESSMENT) 12EXERCISE - PART-A (Section-II)
20 Videos
- SAMPLE PAPER (SELF ASSESSMENT) 12BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER (SELF ASSESSMENT) 12EXERCISE - PART-B (Section-III)
8 Videos
- SAMPLE PAPER 5 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 5 EXERCISE - Part B (Section - V)
4 Videos
- SAMPLE PAPER - 11BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER - 11EXERCISE - SECTION-C
10 Videos
Similar Questions
A crane stands on a level ground. It is represented by a tower ABCD, of height 11 m and a jib BR. The ib is of length 20 m and can rotate in a vertical plane about B.A vertical cable, RS, carries a load S. the diagram shows current position of the jib, cable and load.
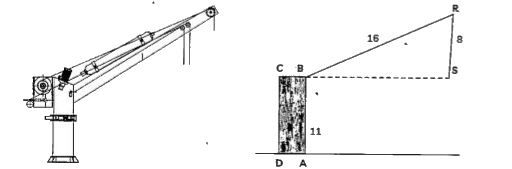
The length BS is
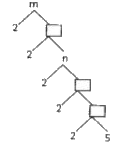
View SolutionIn the adjoining factor tree, find the numbers m and n.
View SolutionSolve: 4x−y=5,x+y=5.
View SolutionThe lower part of the metallic container is right circular cylinder and its lid is hemispherical. The volume of the cylinder is 942cm3 and height is 3 cm. The diameter of the cylinder and the hemisphere is same. Find the area of the sheet for preparing the container. (π=3.14)
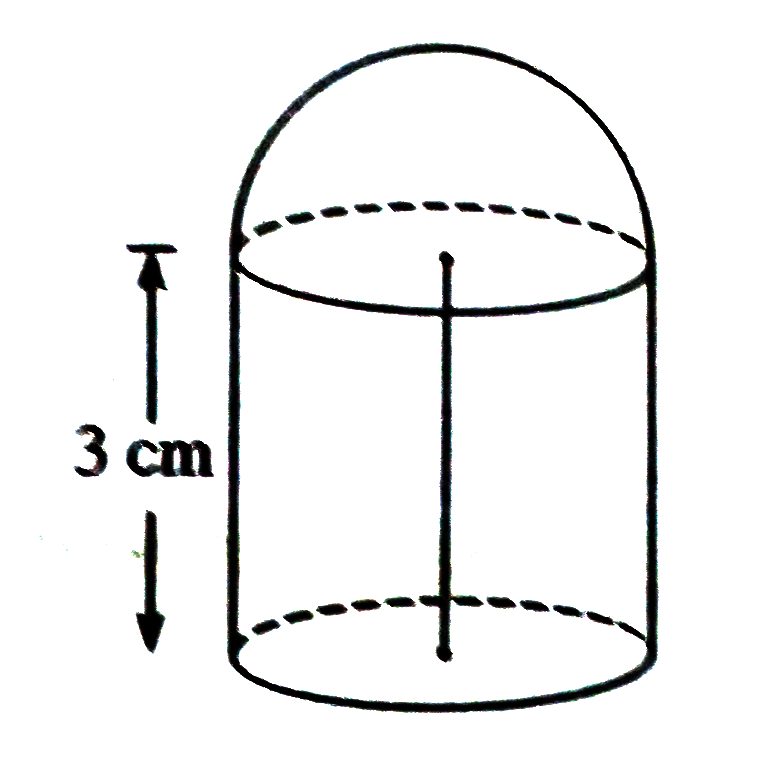
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, 3) and B is (1, 4).
View Solutionबिन्दु A के निद्देशांक ज्ञात कीजिए, जहाँ AB एक वृत्त का व्यास है जिसका कैंद्र (2,-3) है तथा बिंदु B(1,4) है।
View SolutionFind the coordinates of a point A , where AB is the diameter of a circle whose centre is ( 2 , - 3) and B is ( 1 , 4) . (AS4)
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2,−3) and B is (1,4).
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, 3) and B is (1, 4).
View SolutionFind the coordinates of a points A, where AB is the diameter of circle whose centre is (2,-3) and B is (1, 4)
View SolutionFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
View Solution
