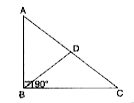
A triangular field BAD, right angled at A has AB=180m and ∠DBA=30∘. The length BD is
198 m
208 m
228 m
243 m
The correct Answer is:B
To find the length of BD in the triangular field BAD, we will use trigonometric ratios. Here are the steps to solve the problem:
Step 1: Identify the triangle and given values
We have a right-angled triangle BAD with the right angle at A. The lengths and angles given are:
- AB = 180 m
- Angle DBA = 30°
Step 2: Use the cosine ratio
In triangle BAD, we can use the cosine of angle DBA to relate the sides. The cosine of an angle in a right triangle is defined as:
cos(θ)=AdjacentHypotenuse
Here, angle DBA is 30°, AB is the adjacent side, and BD is the hypotenuse.
Step 3: Write the cosine equation
Using the cosine ratio for angle DBA:
cos(30∘)=ABBD
Substituting the known values:
cos(30∘)=180BD
Step 4: Substitute the value of cos(30°)
The value of cos(30∘) is √32. Therefore, we can write:
√32=180BD
Step 5: Cross-multiply to solve for BD
Cross-multiplying gives us:
BD⋅√32=180
To isolate BD, we can rearrange the equation:
BD=180⋅2√3
BD=360√3
Step 6: Rationalize the denominator
To simplify, we can multiply the numerator and denominator by √3:
BD=360√33
BD=120√3 m
Final Answer
The length of BD is 120√3 meters.
---
We have a right-angled triangle BAD with the right angle at A. The lengths and angles given are:
- AB = 180 m
- Angle DBA = 30°
In triangle BAD, we can use the cosine of angle DBA to relate the sides. The cosine of an angle in a right triangle is defined as:
cos(θ)=AdjacentHypotenuse
Here, angle DBA is 30°, AB is the adjacent side, and BD is the hypotenuse.
Using the cosine ratio for angle DBA:
cos(30∘)=ABBD
Substituting the known values:
cos(30∘)=180BD
The value of cos(30∘) is √32. Therefore, we can write:
√32=180BD
Cross-multiplying gives us:
BD⋅√32=180
To isolate BD, we can rearrange the equation:
BD=180⋅2√3
BD=360√3
To simplify, we can multiply the numerator and denominator by √3:
BD=360√33
BD=120√3 m
The length of BD is 120√3 meters.
Topper's Solved these Questions
- SAMPLE PAPER -6 Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER -6 Exercise:Part - B (Section - III)
Explore 9 Videos
- SAMPLE PAPER -6 Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER -6 Exercise:Part - B (Section - IV)
Explore 9 Videos
- SAMPLE PAPER -6 Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER -6 Exercise:Part - B (Section - V)
Explore 6 Videos
- SAMPLE PAPER -5Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER -5Exercise:SECTION-C
Explore 11 Videos
- SAMPLE PAPER 01Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 01Exercise:PART-B (SECTION-V)
Explore 4 Videos
Similar Questions
Knowledge Check
A triangular field BAD, right angled at A has AB=180m and ∠DBA=30∘. The length AD is
A29√3B38√3mC43√3 mD60√3mA triangular field ABC, right angled at A has length AC=33m and AB=180m. The length of the side BC is
A193 mB189 mC188 mD183 mA triangular field right angled at A has length AC=33m and AB=180m. The area ( in sq m) of the field ABC is
A2790 sq mB2970 sq mC3102 sq mD3210 sq m
In a right angled triangle, right-angled at A, the angle formed at B is 45∘, if the length of side AB is 3m, then what is the length of the side BC?
View SolutionThe perpendicular sides of a right angled triangle are 3x and 4x. The length of its hypotenuse is 30. Find the lengths of the perpendicular sides of the right angled triangle.
View SolutionABC is a right angled triangle, right angled at C. If ∠A=60∘andAB=40 unit, then the length of AC is
View SolutionABC is a right angled triangle, right angled at C. If ∠A=60∘andAB=40 unit, then the length of AC is
View SolutionIn ΔABC,∠B is a right angle, AC=6 cm, D is the mid point of AC. The length of BD is
View Solution