Two coils have a mutual inductance 0.005H. The current changes in the first coil according to equation I=I0sinωt, where I0=10A and ω=100πradian//sec. The maximum value of e.m.f. in the second coil is
2πV
5πV
πV
4πV
The correct Answer is:B
According to Faraday.s law of induction
e=Mdidt=Md(I0sin(ωt))dt
On differentiating we get
=0.005×I0ωcosωt
on comparing with equation
e=emaxcos(ωt)
We get maximum value of
∴emax=0.005×10×100π
=5πV
[:,cosωt=1]
Topper's Solved these Questions
Similar Questions
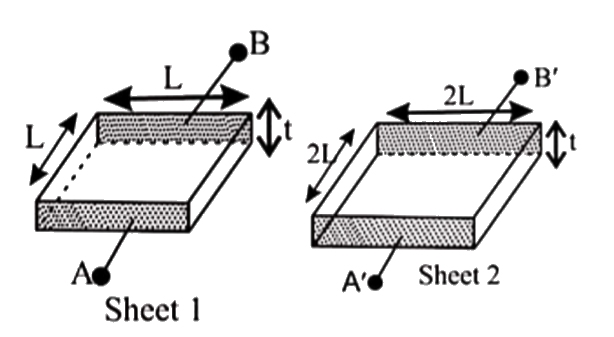
The resistance of metal sheet 1 between A and B is R1 and the resistance of sheet 2 between A' and B' is R2. The value of the ratio R1R2 is
View SolutionIf N0 is the original mass of the substance of half - life period t1/2=5year then the amount of substance left after 15 year is
View SolutionTwo coils have a mutual inductance of 0.005 H . the current changes in the first coil according to equation I=I_0 sinomegat , where I_0=10A and omega=100pirad//s . The maximum value of emf (in volt) in the second coil is
View SolutionTwo coils have a mutual inductance 0.005 H . The current changes in the first coil according to equation I=I_(0)sin omegat , where I_(0)=10A and omega=100pi radian//sec . The maximum value of e.m.f. in the second coil is
View SolutionTwo coils have a mutual inductance 0.005H. The current changes in the first coil according to the equation I=I_(0) sin omegat "where" I_(0)=10A and omega =100pi rad//s . The maximum value of emf wiin second coil is (pi//x) volts. Find the value of x.
View SolutionTwo coils have the mutual inductance of 0.05 H. The current changes in the first coil as I=I_(0)sin omegat , where I_(0)=1A and omega=100pi"rad/s" . The maximum emf induced in secondary coil is
View SolutionTwo coils have a mutual inductance of 5 xx 10^(-3) H . The current changes in the first coil according to the euquation, I_(1)=I_(0)sin omega t where I_(0)=10A and omega = 100 pi rad//s . What is the value of the maximum e.m.f in the second coil?
View SolutionTwo coils have mutual inductance 0.005 H. The current changes in the first coil according to equation I=I0 sin ωt, where I0=10A and ω=100π rad s−1. The maximum value of induced emf in the second coil is
View SolutionTwo coils have a mutual inductance 0.005 H, The current changes in the first coil according to the equation i= i_(m) sin omega t where i_(m) = 10 A and omega= 100pi rad s^(-1) . The maximum value of the emf induced in the second coil is
View SolutionTwo coils have a mutual inductance of 0.005H. The current changes in the first coil according to equation I=I0sinωt , where I0 = 10A and ω=100π rad/sec. The maximum value of emf in the second coil is ___
View SolutionTwo coils have a mutual inductance 0.005 H. The current changes in the first coil according to the equation I=I0sinωtwhereI0=10Aandω=100πrads−1. The maximum value of emf induced in the second coil is
View SolutionTwo coils have a mutual inductance 0.005 H. The current changes in the first coil according to equation I=I0sinωt, where I0=10A and ω=100π rad/s. The maximum value of e.m.f. in the second coil is
View SolutionTwo coils have a mutual inductance of 0.005 H . the current changes in the first coil according to equation I=I_0 sinomegat , where I_0=10A and omega=100pirad//s . The maximum value of emf (in volt) in the second coil is
View SolutionTwo coils have a mutual inductance 0.005H. The current changes in the first coil according to the equation I=I0sinωtwhereI0=10Aandω=100πrad/s . The maximum value of emf wiin second coil is (pi//x) volts. Find the value of x.
View SolutionTwo coils have a mutual inductance 0.005 H . The current changes in the first coil according to equation I=I_(0)sin omegat , where I_(0)=10A and omega=100pi radian//sec . The maximum value of e.m.f. in the second coil is
View SolutionTwo coils have the mutual inductance of 0.05 H. The current changes in the first coil as I=I0sinωt, where I0=1A and ω=100πrad/s. The maximum emf induced in secondary coil is
View Solution

