If sinA+sin2A=1, then the value of cos2A+cos4A is 2 (b) 1 (c) -2 (d) 0
1
0
−1
oo
Step by step video solution for If sinA+sin^2A=1, then the value of cos^2A+cos^4A is 2 (b) 1 (c) -2 (d) 0 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 9 (SELF-ASSESSMENT)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 (SELF-ASSESSMENT)EXERCISE - Section-C (Case Study Based Questions)
10 Videos
- SAMPLE PAPER 9 (SELF-ASSESSMENT)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 (SELF-ASSESSMENT)EXERCISE - Section-C (Case Study Based Questions)
10 Videos
- SAMPLE PAPER 9BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9EXERCISE - SECTION C
10 Videos
- SAMPLE PAPER SELF ASSESSMENT 11BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER SELF ASSESSMENT 11EXERCISE - Section (iv)
13 Videos
Similar Questions
For teaching the concept of probability, Mrs. Verma decided to use two dice. Shet took a pair of die and write all the possible outcomes on the blackboard. All possible outcomes wave:

(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)
The probability that 4 will not come up on either of them is
View SolutionFor teaching the concept of probability, Mrs. Verma decided to use two dice. Shet took a pair of die and write all the possible outcomes on the blackboard. All possible outcomes wave:

(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2,1), (2,2), (2,3), (2,4), (2,5), (2,6)
(3,1), (3,2), (3,3), (3,4), (3,5), (3,6)
(4,1), (4,2), (4,3), (4,4), (4,5), (4,6)
(5,1), (5,2), (5,3), (5,4), (5,5), (5,6)
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)
The probability that 4 will not come up on either of them is
View SolutionCase Study-1:
Due to covid-19 lockdown, Ramesh decides to redo his house garden with some plantation work with his son. They have an equilateral triangle shaped garden and he has planted the garden with 6 different types of flowers (each of radius 1 m within a circular area). This left the remaining part of garden (that is outside the circular plants area) with lush green grass.
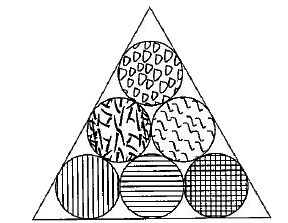
Now, comes the part of adding boundaries to corner the garden off nicely and he needs to know some calculations for it.
A boundary wall of height 25 cm is to be made around the garden leaving a space of 1 m wide for a gate on one side. The total length of boundary wall is
View SolutionProve that : cos2θ1−tanθ+sin3θsinθ−cosθ=1+sinθcosθ
View SolutionIf A=⎡⎢⎣2000cossinx0−sinxcosx⎤⎥⎦ then (AdjA)−1= (A) 12A (B) A (C) 2A (D) 4A
View Solutionsin^4A-cos^4A=2sin^2A-1=1-2cos^2A=sin^2A-cos^2A
View SolutionIf sinA=35, where 0∘<A<90∘, find the values of sin2A,cos2A,tan2A and sin4A.
View SolutionIf sinA+sin2A=1, then the value of cos2A+cos4A is
View SolutionIf sinA+sin2A=1, then the value of cos2A+cos4A is (a)2 (b) 1 (c) -2 (d) 0
View SolutionProve the following identities: sin4A−cos4A=sin2A−cos2A=2sin2A−1=1−2cos2A
View SolutionIf cosA+cos2A=1, find the value of sin2A+sin4A.
View Solutioncos4A−sin4A is equal to
(a)2cos2A+1
(b) 2cos2A−1
(c) 2sin2A−1
(d) 2sin2A+1
View SolutionIf cosA+cos2A=1 , then sin2A+sin4A=
(a)−1
(b) 0
(c) 1
(d) None of these
View Solutionsin6A+cos6A+3sin2Acos2A= a. 0 b. 1 c. 2 d. 3
View SolutionsinA+cosAsinA−cosA+sinA−cosAsinA+cosA=2sin2A−cos2A=21−2cos2A=2sin2A−1 .
View SolutionIf sin4A−cos2A=cos4A−sin2A(0<A<π4), then the value of tan4A=................. A) 1 B) 1√3 C) √3 D) √3−1√3+1
View Solution
