The corner points of the feasible region of a LPP are (20,0),(10,50),(0,60) and (0,0). If Z= 50x +15y, then maximum value of Z occurs at :
(20,0)
(10,50)
(0.60)
(0,0)
The correct Answer is:B
Topper's Solved these Questions
- SAMPLE PAPER 6 Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 6 Exercise:SECTION -B
Explore 20 Videos
- SAMPLE PAPER 6 Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 6 Exercise:SECTION - C
Explore 9 Videos
- SAMPLE PAPER 4 Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 4 Exercise:SECTION - C
Explore 7 Videos
- SAMPLE PAPER 7Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 7Exercise:SECTION -C
Explore 10 Videos
Similar Questions
If A=[α011]andB=[1021] such that A2=B, then what is the value of α ?
View SolutionLet R be the relation in the set N given by R = {a,b):a is a multiple of b} .Then :
View SolutionThe feasible region for an LPP is shown in the Let Z = 4x + 3y be the objective function. Maximum of Z occur at :
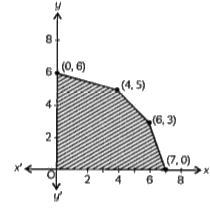
View SolutionWhich of the following is correct regarding f(x) =x3 ?
View SolutionThe feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists

View SolutionMaximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
View SolutionConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?
View SolutionThe corner points of the feasible region of an LPP are (0,0), (0,8), (2,7),(5,4),and (6,4). the maximum profit P= 3x + 2y occurs at the point_____.
View SolutionThe feasible region of an LPP is shown in the figure. If Z=11x+7y, thent he maximum value of Z occurs at

View SolutionThe feasible region of an LPP is shown in the figure. If z = 3x + 9 y , then the minimum value of z occurs at
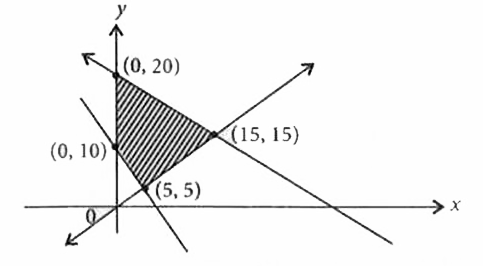
View SolutionThe feasible region of an LPP is shown in the figure. If z=3x+9y ,then the minimum value of z occurs at
View SolutionThe feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists

View SolutionMaximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
View SolutionThe corner points of the feasible region of an LPP are (0,0), (0,8), (2,7),(5,4),and (6,4). the maximum profit P= 3x + 2y occurs at the point_____.
View Solution

