If set A has 3 elements and the set B has 5 elements , then , the number of injective mappings that can be defined from A to B is :
60
120
240
360
The correct Answer is:A
To find the number of injective mappings (one-to-one functions) from set A to set B, we can follow these steps:
1. Identify the sizes of the sets:
- Set A has 3 elements.
- Set B has 5 elements.
2. Understand the concept of injective mappings:
An injective mapping means that each element in set A must map to a unique element in set B. No two elements in set A can map to the same element in set B.
3. Choose an element from set B for each element in set A:
- For the first element in set A (let's call it A1), we have 5 choices from set B (U, V, W, X, Y).
- For the second element in set A (A2), since we cannot use the element already chosen for A1, we have 4 remaining choices.
- For the third element in set A (A3), we cannot use the elements chosen for A1 and A2, leaving us with 3 choices.
4. Calculate the total number of injective mappings:
The total number of injective mappings can be calculated by multiplying the number of choices for each element:
Total injective mappings=5×4×3
5. Perform the multiplication:
5×4=20
20×3=60
6. Conclusion:
Therefore, the total number of injective mappings from set A to set B is 60.
Summary of Steps:
1. Identify the sizes of sets A and B.
2. Understand injective mappings.
3. Choose elements from set B for each element in set A.
4. Calculate the total number of mappings by multiplying the choices.
5. Perform the multiplication to get the final answer.
- Set A has 3 elements.
- Set B has 5 elements.
An injective mapping means that each element in set A must map to a unique element in set B. No two elements in set A can map to the same element in set B.
- For the first element in set A (let's call it A1), we have 5 choices from set B (U, V, W, X, Y).
- For the second element in set A (A2), since we cannot use the element already chosen for A1, we have 4 remaining choices.
- For the third element in set A (A3), we cannot use the elements chosen for A1 and A2, leaving us with 3 choices.
The total number of injective mappings can be calculated by multiplying the number of choices for each element:
Total injective mappings=5×4×3
5×4=20
20×3=60
Therefore, the total number of injective mappings from set A to set B is 60.
1. Identify the sizes of sets A and B.
2. Understand injective mappings.
3. Choose elements from set B for each element in set A.
4. Calculate the total number of mappings by multiplying the choices.
5. Perform the multiplication to get the final answer.
Topper's Solved these Questions
- SAMPLE PAPER 6 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6 EXERCISE - SECTION - C
9 Videos
- SAMPLE PAPER 6 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6 EXERCISE - SECTION - C
9 Videos
- SAMPLE PAPER 4 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 4 EXERCISE - SECTION - C
7 Videos
- SAMPLE PAPER 7BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - SECTION -C
10 Videos
Similar Questions
Let R be the relation in the set N given by R = {a,b):a is a multiple of b} .Then :
View SolutionLet R be the relation in the set N given by R = {a,b):a is a multiple of b} .Then :
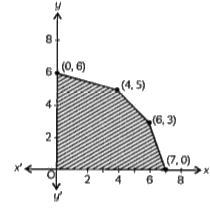
View SolutionThe feasible region for an LPP is shown in the Let Z = 4x + 3y be the objective function. Maximum of Z occur at :
View SolutionWhich of the following is correct regarding f(x) =x3 ?
View SolutionSet A has three elements and set B has four elements.The number of injections that can be defined from A to B is
View SolutionSet A has 5 eleements and set B has 3 elements. Find the number of relations from set A to B.
View SolutionFind the number of injections of a set A with 5 elements to a set B with 7 elements.
View SolutionSet A has 3 elements and set B has 4 elements. The number of injections that can be defined from A to B is
View SolutionSet A has 3 elements and set B has 4 elements. The number of injections that can be defined from A into B is
View SolutionThe set A has 4 element and the set B has 5 elements then the number of injective mappings that can be deifned from A to B is
View SolutionIf a set A has 3 elements and B has 5 elements, find the number of injections from A to B.
View SolutionA set A has 3 elements and a set B has 4 elements . The number of one one function defined from set A to B is .........
View SolutionSet A has 3 elements. Set B has 4 elements. The number of surjections that can be defined from A to B is
View Solutionसमुच्चय A में 3 तथा B में 4 अवयव है तब A से B में बनने वाले एकैकी प्रतिचित्रणों की संख्या होगी
View Solutionयदि समुच्चय A में 5 अवयव हैं तथा समुच्चय B में 6 अवयव हैं, तो A से B में एकैकी तथा आच्छादक प्रतिचित्रणों की संख्या
View SolutionSet A has 3 elements and set B has 4 elements. The number of injections that can be defined from A to B is
View Solution

