Let a, b, c, be three rational numbers, where a=35,b=23andc=−56 . Which one of the following is true
a÷(a÷c)=b÷(a+c)
a÷(b+c)=c÷(a+b)
a−(b−c)=c−(a−b)
a×(b+c)=b×(a÷c)
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
As per NCF 2005, one main goal of Mathematics education in schools is to
View SolutionThe following observations were made by students A, B, C and D when they rubbed solid baking soda on dry litmus paper:

The correct observation was made by the student
View SolutionAHNO2−−−→C2H5OH[O]−−→B में A तथा B को पहचान-कर उनके सूत्र एव नाम लिखिए।
View Solutionनिम्नलिखित अभिक्रियाओं में योगिक [A] तथा [B] को पहचानिए तथा सम्बंधित संतुलित रासायनिक समीकरण भी लिखिए -
CH3CONH2P2O5−−−−−→Δ[A]4[H]−−−−−−−−−→Na+C2H5OH[B]
View Solutiona और b के लिये हल कौजिए :
2a+3b=17 और 2a+2−3b+1=5
View Solutionएक DetlaABC में ∠C=3∠B=2(∠A+∠B) है । त्रिभुज के तीनो कोण ज्ञात कीजिए।
View Solutionहल कीजिए: a+aba=y+abb और ax+by=a3+b3
View Solutionc को दो भगो में एक प्रकार सोने की छड़ बन जाए ? कीजिए की बड़े भाग का 'a ' गुना छोटे भाग के 'b ' गुने के बराबर है ।
View Solutionयदि 10 टिकटों पर 1 से 10 तक की (प्रत्येक पर एक) संख्यायें लिखी हुई हैं। कोई संख्या दोहराई नहीं गई है। यदि A एक ऐसी घटना है, जिसमें विषम संख्यायें हों और B एक ऐसी घटना हो, जिसमें 3 से विभाज्य संख्या हों, तो दिखाओ कि P(A∪B)=P(A)+P(B)−P(A∪B)
View Solutionतीन तत्व A, B और C एक घनीय ठोस जलक में क्रिस्टलीकृत होते हैं । परमाणु A कोनो पर परमाणु B घन के केंद्र पर तथा परमाणु C किनारो पर स्थित होते हैं । यौगिक का सूत्र होगा :
View Solutionसाबित करें कि
sin(B−C)cosBcosC+sin(C−A)cosCcosA+sin(A−B)cosAcosB=0
View Solutionबहुपद f(x)=ax2+bx+c का आलेखः चित्र में दर्शाया गया है | 'a' तथा b2−4ac के चिन्ह लिखिए |
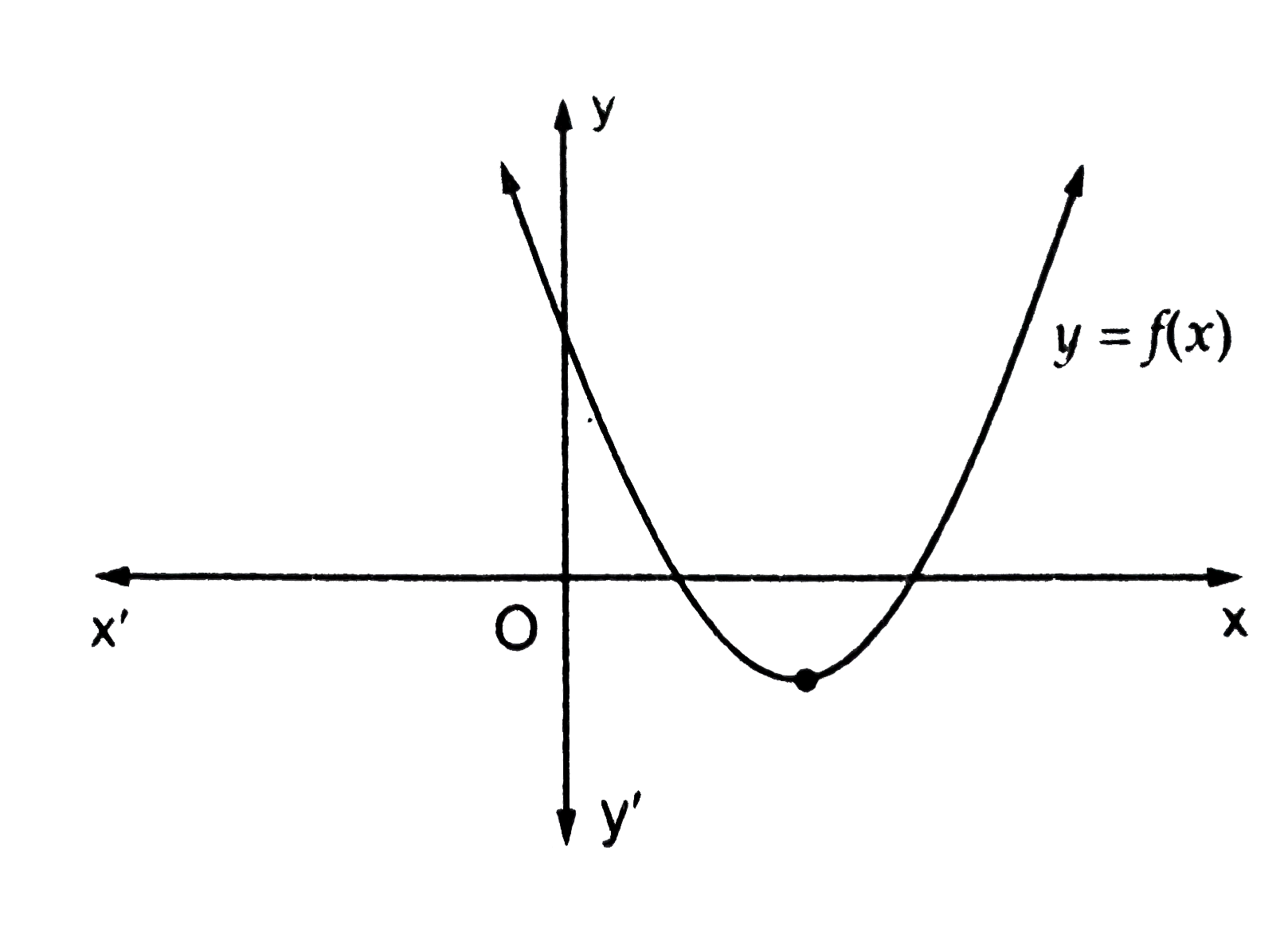
View Solutionयदि a−b,a तथा a + b , बहुपद f(x)=2x3−6x2+5x−7 के शून्यक हो, तो 'a' का मान लिखिए |
View Solutionयदि (secA+tanA)(secB+tanB)(secC+tanC)
=(secA−tanA)(secB−tanB)(secC−tanC) हो, तो सिद्ध करो की प्रत्येक पक्ष ±1के बराबर है।
View Solutionयदि acosθ−bsinθ=c तो, प्रमाणित करो कि
asinθ+bcosθ=±√a2+b2−c2
View SolutionFive numbers a,b,c,d and e are in the ratio of 2:3:5:8:9 and their sum is 162. Find the average of all these numbers:
View Solution
