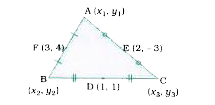
If the coordinates of the mid-points of the sides of a triangle are (1,1),(2,-3) and (3,4), then the excentre opposite to the vertex A is
(−20√2+2√13−5√2−√13+√17,8√13−6√17−5√2+√13+√17)
(−20√2+2√135√2+√13+√17,8√13−6√17−5√2+√13+√17)
(−20√2+2√13−5√2+√13+√17,8√13−6√17−5√2+√13+√17)
None of the above
The correct Answer is:C
Similar Questions
The coordinates of the mid -point of the sides of a triangle are (0,1) (1,1)and (1,0),find the coordinates of the triangle.
View SolutionIf the coordinate of the mid - point of the sides AB, BC and CA of a trinagle are (3,4) (1,1) and (2,-3) respectively , then the vertice A and B of the triangle are .
View SolutionA _____ connects a vertex of a triangle to the mid point of the opposite side.
View SolutionIf the coordinates of the mid points of the sides of a triangle are (1,1) ,(2,-3) and (3,4) . Find its centroid :
View SolutionIf the coordinates of the mid points of the sides of a triangle are (1,1) ,(2,-3) and (3,4) .Find the centroid for the given triangle :
View SolutionIf the coordinates of the mid-points of the sides of a triangle are (1,1),(2,−3)and(3,4). Find its (i) centroid (ii) in-centre.
View SolutionIf the coordinates of the mid-points of the sides of a triangle are (1,1),(2,−3)and(3,4) . Find its centroid.
View SolutionIf the coordinates of the midpoints of the sides of ΔABC are (1,1), (2,-3) and (3,4) , find the coordinates of the vertices of ΔABC
View Solution

