How are stationary waves formed in closed pipes ? Explain the various modes of vibrations and obtain the relations for the frequencies.'
A closed organ pipe 70 cm long is sounded. If the velocity of sound is 331.m/s, what is the fundamental frequency of vibration of the air column ?
A closed pipe is a cylindrical tube having air inside it with one end closed and the other end open.
Let a longitudinal wave be sent through a closed pipe. It gets, reflected at the closed end of the pipe. These incident and reflected waves, which are of same frequency, travelling in opposite directions-gets superposed as a result longitudinal stationary waves are formed."
At the closed end reflection is on a rigid surface a node is formed at closed end, at the open end antinode is formed.
1. Harmonics in a closed pipe :
Fundamental mode (or) First Harmonic:
In this one node and one antinode is formed. If . l. is the vibrating length and λ1 is the corresponding wavelength
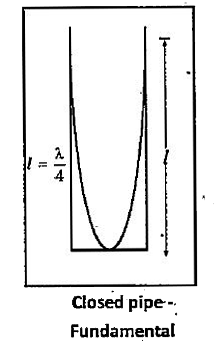
l=λ14 because the distance between a node and next antinode is λ4
λ1=4l
The fundamental frequency
υ1=vλ1⇒υ=v4l
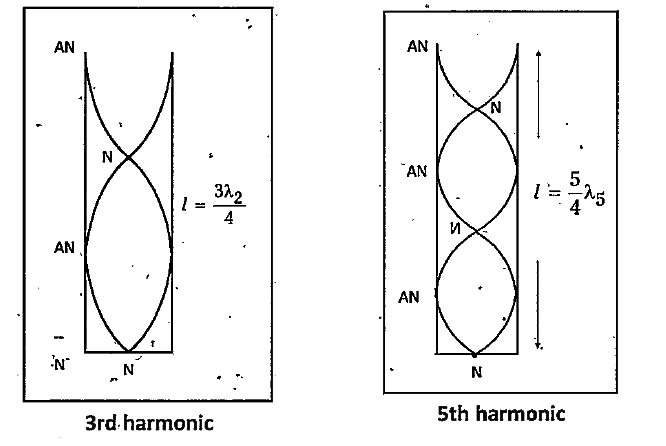
II. First overtone or 2nd Harmonic:
1st overtone consists of two nodes and two antinodes are formed. If./. is the vibrating length and λ3 is the corresponding wavelength l=λ4+λ2
The frequency of the first overtone or 3rd harmonic
υ3=vλ3=3v4l,υ3=3υ1
III., Fifth Harmonic or 3rd overtone:
2nd overtone consists of three nodes and three antinodes are formed. If .r is the vibrating length, λ5 is the corresponding wave length,
l=λ54+λ52+λ52=5λ54
The frequency of second overtone or 5th harmonic
υ5=vλ5⇒υ5=5v4l,υ5=5υ1
In closed pipe Harmonics are in the ratio = 1:3:5:7 ...... In closed pipe only odd Harmonics are formed.
Problem
Length of closed organ pipe l = 70 cm
Velocity of sound v= 331 ms−1
Fundamental frequency of closed pipe
υ=v4l=3314×70×10−2=331280×10−2
n=331×102280
n = 118.2 Hz
Topper's Solved these Questions
Similar Questions
Calculate the fundamental frequency of an organ pipe, of length 0.8 m open at both ends if the velocity of sound in air is 330 m/s. What will be the fundamental frequency if one end of the pipe is closed ?
View SolutionCalculate the frequency of fifth harmonic of a closed organ pipe of length 50cm, if the velocity of sound in air is 330 m/s.
View Solution
Knowledge Check
If the velocity of sound in air is 350 m/s . Then the fundamental frequency of an open organ pipe of length 50 cm, will be
A350 HzB175 HzC900 HzD750 HzIf the speed of sound in air is 320m/s, then the fundamental frequency of an closed pipe of length 50cm , will be
A320HzB160HzC640HzD960HzAn open organ pipe of length is 50 cm, if the velocity of sound in air is 320m/s , then the frequency of its fundamental note will be
A160HzB480HzC320HzD640Hz
Calculate the frequency of fifth harmonic of a closed organ pipe of length 50cm, if the velocity of sound in air is 330 m/s.
View SolutionCalculate the frequency of fifth harmonic of a closed organ pipe of length 50cm, if the velocity of sound in air is 330 m/s.
View SolutionCalculate the frequency of fifth harmonic of a closed organ pipe of length 50cm, if the velocity of sound in air is 330 m/s.
View SolutionWhat is the fundamental frequency of an open organ pipe of length 42.5 cm, if the velocity of sound in air is 340 m/s?
View SolutionWhat is the fundamental frequency of an open organ pipe of length 42.5 cm, if the velocity of sound in air is 340 m/s?
View Solution

