A person crossing a road with a certain velocity due north sees a car moving towards east The relative velocity of the car w.r.t the person is √2 times that fo the velocity of the persons. The angle made by the relative velocity with the east is
30∘
45∘
60∘
90∘
The correct Answer is:B
To solve the problem, we need to analyze the motion of the person and the car in terms of their velocities and the relative velocity between them.
1. Define the Velocities:
- Let the velocity of the person (moving due north) be →vp=u^j.
- Let the velocity of the car (moving due east) be →vc=v^i.
2. Relative Velocity:
- The relative velocity of the car with respect to the person is given by:
→vcp=→vc−→vp=v^i−u^j
3. Magnitude of Relative Velocity:
- The magnitude of the relative velocity |→vcp| can be calculated using the Pythagorean theorem:
|→vcp|=√v2+u2
4. Given Condition:
- According to the problem, the magnitude of the relative velocity is √2 times the velocity of the person:
|→vcp|=√2u
- Therefore, we have:
√v2+u2=√2u
5. Square Both Sides:
- Squaring both sides gives:
v2+u2=2u2
- Simplifying this, we find:
v2=u2
6. Relationship Between Velocities:
- From v2=u2, we conclude that:
v=u
7. Finding the Angle:
- The relative velocity vector can now be expressed as:
→vcp=v^i−v^j=v(^i−^j)
- The angle θ that this vector makes with the east (the positive x-axis) can be found using the tangent function:
tanθ=OppositeAdjacent=vv=1
- Therefore, the angle θ is:
θ=tan−1(1)=45∘
Final Answer:
The angle made by the relative velocity with the east is 45∘.
---
- Let the velocity of the person (moving due north) be →vp=u^j.
- Let the velocity of the car (moving due east) be →vc=v^i.
- The relative velocity of the car with respect to the person is given by:
→vcp=→vc−→vp=v^i−u^j
- The magnitude of the relative velocity |→vcp| can be calculated using the Pythagorean theorem:
|→vcp|=√v2+u2
- According to the problem, the magnitude of the relative velocity is √2 times the velocity of the person:
|→vcp|=√2u
- Therefore, we have:
√v2+u2=√2u
- Squaring both sides gives:
v2+u2=2u2
- Simplifying this, we find:
v2=u2
- From v2=u2, we conclude that:
v=u
- The relative velocity vector can now be expressed as:
→vcp=v^i−v^j=v(^i−^j)
- The angle θ that this vector makes with the east (the positive x-axis) can be found using the tangent function:
tanθ=OppositeAdjacent=vv=1
- Therefore, the angle θ is:
θ=tan−1(1)=45∘
The angle made by the relative velocity with the east is 45∘.
Similar Questions
A car is moving with velocity →vc towards north and a train is moving towards east with velocity →vt . Find the direction of relative velocity of car with respect to train.
View SolutionThe velocity-time graph of a car moving along a straight road is shown in figure. The average velocity of the car is first 25 seconds is
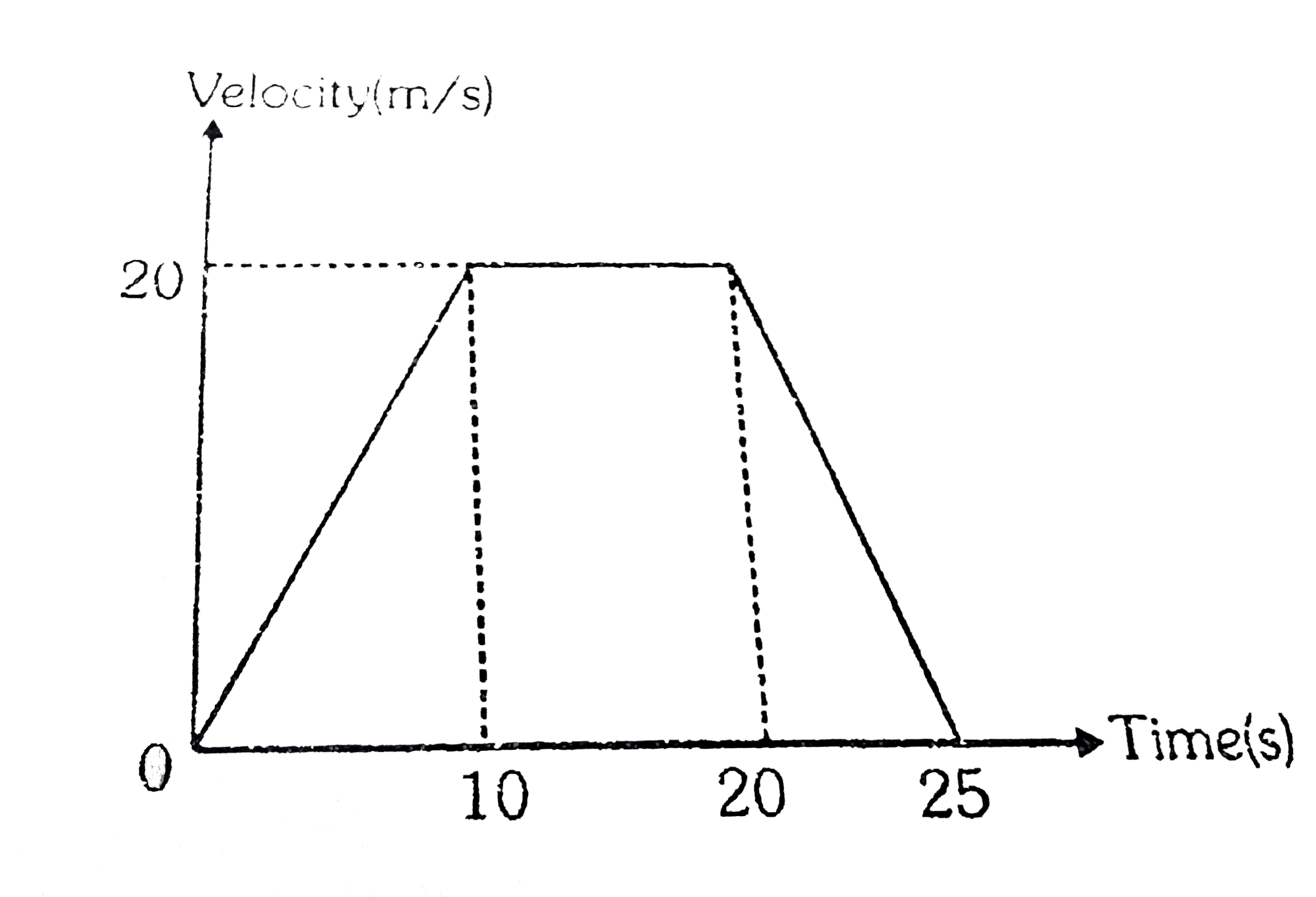
View SolutionThe velocity-time graph of a car moving along a straight road is shown in figure. The average velocity of the car in first 25 seconds is
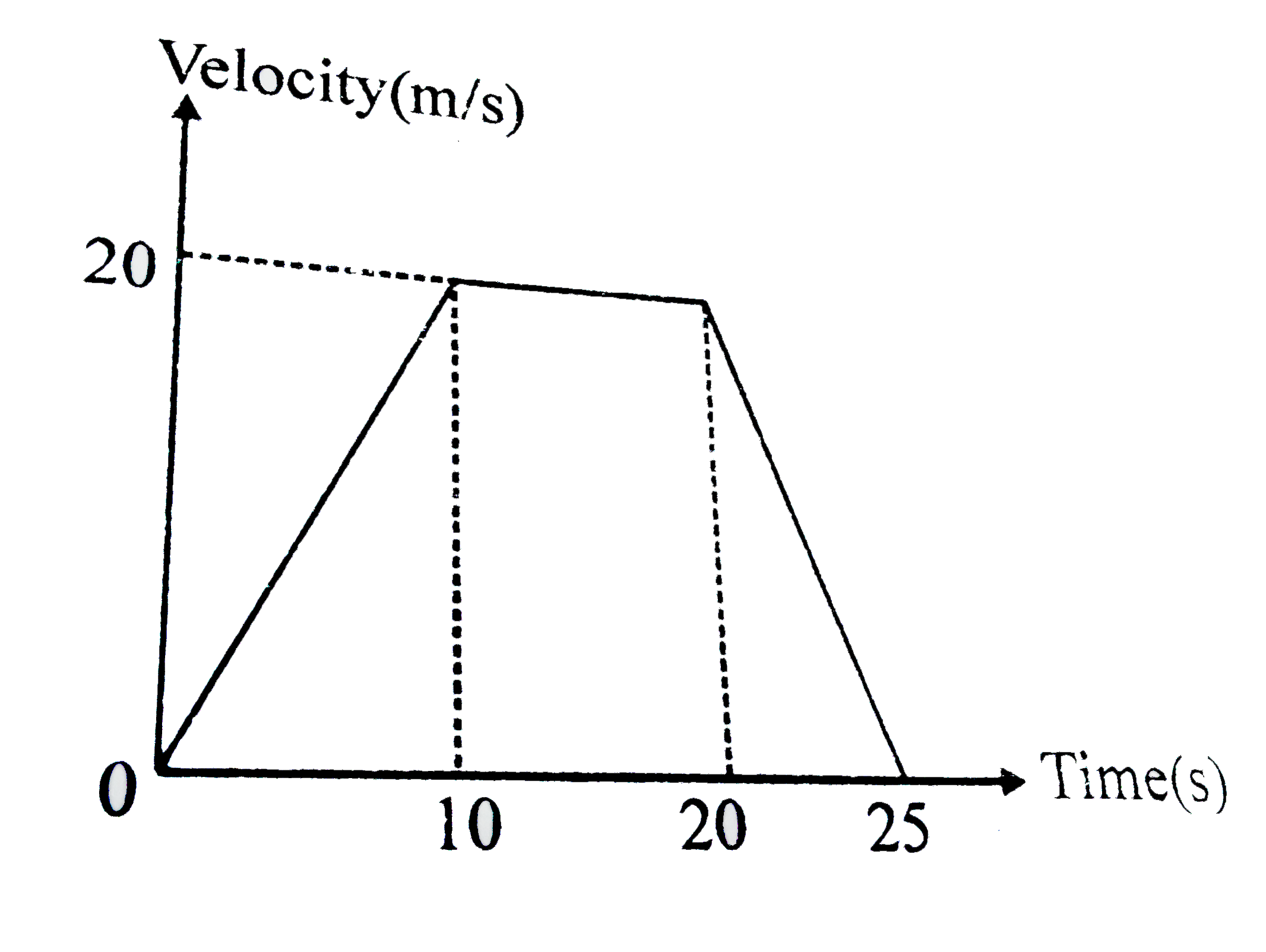
View SolutionA plane mirror and a person are moving towards each other with same velocity v. Then the velocity of the image is
View SolutionThe diagram shows a train moving with constant velocity and a car moving towards the train with constant velocity. The engine driver measures the velocity of the car as v1 . The passenger sitting in the last compartment measures the velocity of the car as v2 . Which of the following statements is true?

View SolutionA car A moves along north with velocity 30 km/h and another car B moves along east with velocity 40 km/h. The relative velocity of A with respect to B is
View SolutionA person driving a car with a speed 72 km/h suddenly sees a boy crossing the road. If the distance moved by car, before the person applies brakes is 5 m, the reaction time of the person is
View SolutionTwo cars are moving is one a same line dimension in opposite direction with the same speed v. The relative velocity of two cars w.r.t. each other is
View SolutionA motorcylcle is moving with a velocity 80km/hr ahead of a car moving with a velocity of 65 km/hr in the same direction. What is the relative velocity of the motorcyle with respect ot the car:-
View SolutionFind the velocity of the image when a plane mirror and a person are moving towards each other with same velocity v.
View Solution
