Consider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

2,25,∞
1,∞,34
1,∞,30
10,∞,20
The correct Answer is:B
Step by step video solution for Consider the situation shown in figure. The two slits S_1 and S_2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength lamda. The separation between the slits is d. The light transmitted by the slits falls on a screen Sigma_1 placed at a distance D from the slits. The slit S_3 is at the placed central line and the slit S_4, is at a distance z from S_3. Another screenSigma_2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Sigma_2 if z is equal to a. z=(lamdaD)/(2d) b. (lamdaD)/d c. (lamdaD)/(4d) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVE OPTICSBook:AAKASH SERIESChapter:WAVE OPTICSExercise:LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) More than one correct answer type questions
Explore 4 Videos
- WAVE OPTICSBook:AAKASH SERIESChapter:WAVE OPTICSExercise:LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) Linked Comprehension type questions
Explore 6 Videos
- WAVE OPTICSBook:AAKASH SERIESChapter:WAVE OPTICSExercise:PROBLEMS (LEVEL - II)
Explore 33 Videos
- WAVE MOTION AND SOUNDBook:AAKASH SERIESChapter:WAVE MOTION AND SOUNDExercise:PROBLEMS (LEVEL - II)
Explore 97 Videos
- WAVESBook:AAKASH SERIESChapter:WAVESExercise:EXERCISE-III (Doppler effect :)
Explore 15 Videos
Similar Questions
If the source of light used in a Young's Double Slit experiment is changed from red to blue, then
View SolutionLight of wavelengthλ=500nm falls on two narrow slits placed a distance d = 50×10−4 cm
apart, at an angle ϕ=30∘ relative to the slits as shown in figure. On the lower slit a transparent slab of thickness 0.1 mm and refractive index 32 is placed. The interference pattern is observed at a distance D=2m from the slits. Then, calculate

(a) position of the central maxima.
(b) the order of maxima at point C of screen .
(c)how many fringes will pass C, if we remove the transparent slab from the lower slit?
View SolutionIn Young's double-slit experiment, the y-coordinate of central maxima and 10th maxima are 2 cm and 5 cm, respectively, When the YDSE apparatus is immersed in a liquid of refractive index 1.5, the corresponding y-coordinates will be
View SolutionA wave is described by the equation y=(1.0mm)sinπ(x2.0cm−t0.01s).
(a) Find time period and wavelength.
(b) Find the speed of particle at x=1.0cm and time t=0.01s.
( c ) What are the speed of the partcle at x=3.0cm, 5.0cmand7.0cm at t=0.01s?
(d) What are the speeds of the partcle at x=1.0cm at t=0.011 , 0.012and0.013s?
View SolutionWhen a train is approaching the stationary observer, the apparent frequency of the whistle observed as 100 Hz, while when it has passed away from the observer with same speed, it is 50 Hz. Calculate the frequency of the whistle when the observer moves with the train V = 330 m/s)
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

View SolutionConsider the situation shown in fig. The two slits S_(1) and S_(2) placed symmetrically around the central line are illuminated by monochromatic light of wavelength lambda . The separation between the slit is d. The ligth transmitted by the slits falls on a screen S_(0) placed at a distance D form the slits. The slit S_(3) is at the central line and the slit S_(4) is at a distance z from S_(3) Another screen S_(c) is placed a further distance D away from S_(c) Find the ratio of the maximum to minimum intensity observed on S_(c) If z = (lambda D)/(2 d)
View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
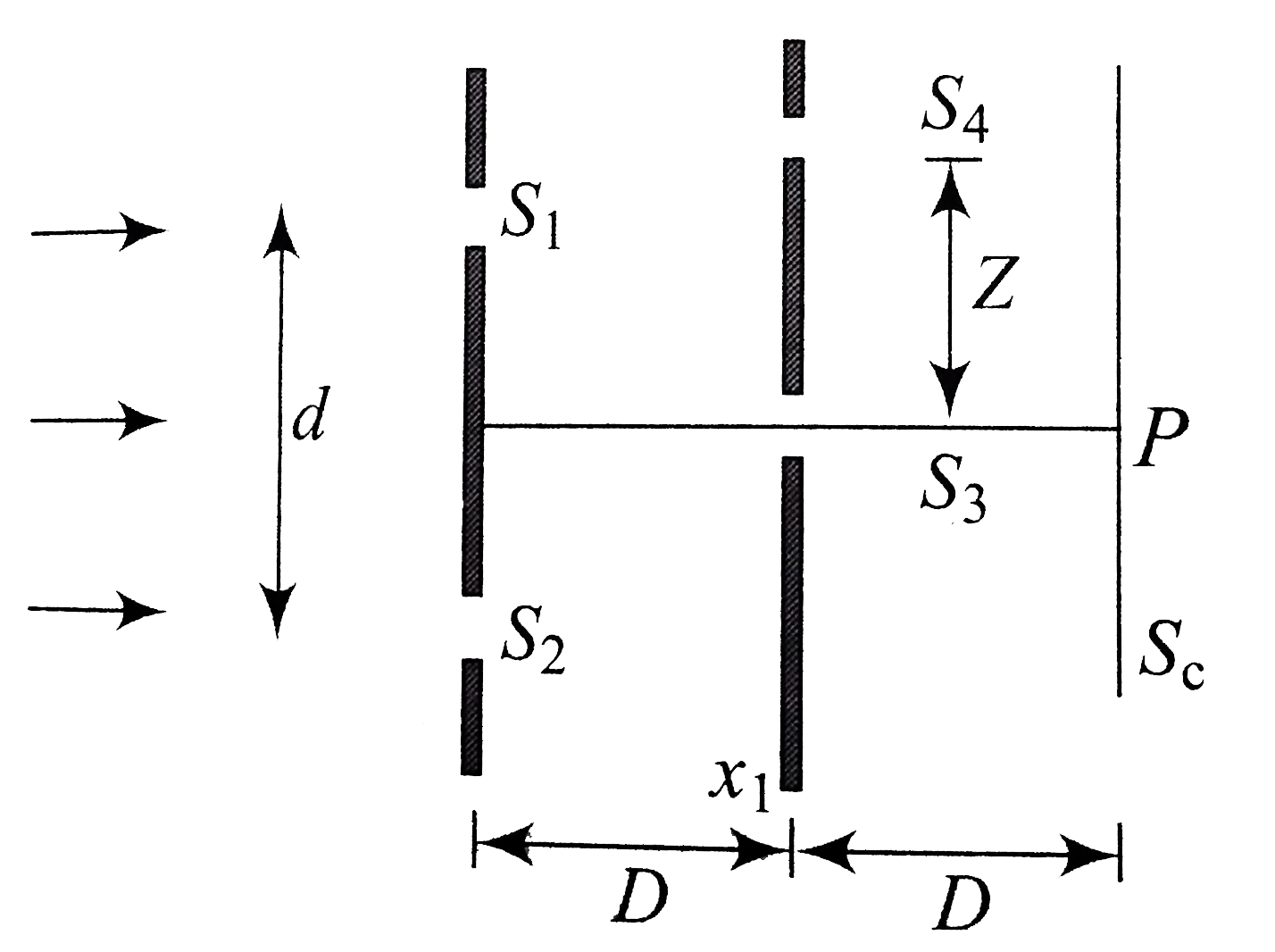
If z=λDd
View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
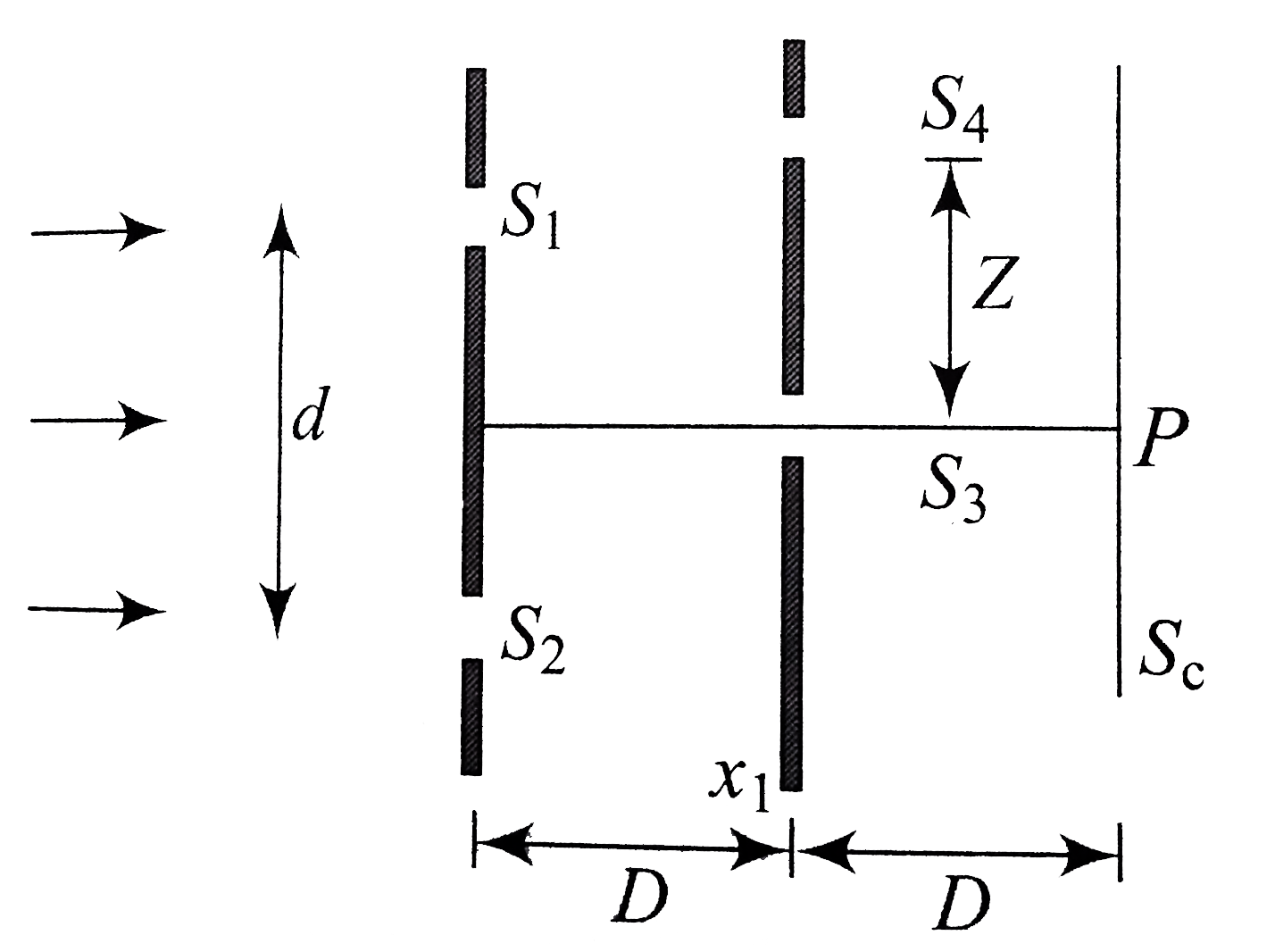
If z=λD4d
View SolutionIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is lambda and I is theintensity of central bright fringe, then intensity at distance from central maximum is
View SolutionConsider the situation shown in figure-6.35. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen E1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen E2 is placed a further distance D away from E1. Find the ratio of the maximum to minimum intensity observed on E2 if z is equal is : (a)λD2d (b)λDd (c)λD4d

View SolutionIn a double slit experiment, the separation between the slits is d and distance of the screen from slits is D. If the wavelength of light used is λ and I is the intensity of central bright fringe, then intensity at distance from central maximum is
View SolutionA light of wavelength λ falls on a narrow slit of width d.A diffraction fringe is formed on a screen placed at distance D from the slit. If the linear width of the central maximum equals to the width of the slit, will be the value of D?
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
View SolutionIn a Young's double slit interference experiment the fringe pattern is observed on a screen placed at a distance D from the slits. The slits are separated by a distance d and are illuminated by monochromatic light of wavelength λ. Find the distance from the central point where the intensity falls to (a) half the maximum, (b) one fourth of the maximum.
View Solution
