The average path difference between two waves coming from third and fifth fresnel zones of a wave front at the centre of the screen is
λ2
2λ
λ
4λ
The correct Answer is:C
To find the average path difference between two waves coming from the third and fifth Fresnel zones at the center of the screen, we can follow these steps:
Step 1: Understand Fresnel Zones
Fresnel zones are regions in the wavefront that contribute to the interference pattern. Each zone is a three-dimensional elliptical region, and the nth Fresnel zone is defined by its radius and the distance from the source.
Step 2: Determine the Path Difference
The path difference between two waves coming from different Fresnel zones can be calculated using the formula:
Δx=(n22−n21)λ2d
where:
- n1 and n2 are the zone numbers (in this case, 3 and 5),
- λ is the wavelength of the waves,
- d is the distance from the source to the observation point.
Step 3: Substitute the Values
For this problem:
- n1=3
- n2=5
- The average path difference becomes:
Δx=(52−32)λ2d
Calculating 52−32:
52=25and32=9⇒25−9=16
Thus, the path difference simplifies to:
Δx=16λ2d=8λd
Step 4: Conclusion
The average path difference between the waves coming from the third and fifth Fresnel zones at the center of the screen is given by:
Δx=8λd
Fresnel zones are regions in the wavefront that contribute to the interference pattern. Each zone is a three-dimensional elliptical region, and the nth Fresnel zone is defined by its radius and the distance from the source.
The path difference between two waves coming from different Fresnel zones can be calculated using the formula:
Δx=(n22−n21)λ2d
where:
- n1 and n2 are the zone numbers (in this case, 3 and 5),
- λ is the wavelength of the waves,
- d is the distance from the source to the observation point.
For this problem:
- n1=3
- n2=5
- The average path difference becomes:
Δx=(52−32)λ2d
Calculating 52−32:
52=25and32=9⇒25−9=16
Thus, the path difference simplifies to:
Δx=16λ2d=8λd
The average path difference between the waves coming from the third and fifth Fresnel zones at the center of the screen is given by:
Δx=8λd
Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET Exercise - II DIFFRACTION (Level - I (Main) Level - II (Straight objective type questions)
8 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET Exercise - III POLARLISATION(Level - I (Main) (Straight objective Type questions))
7 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET (EXERCISE - I) (INTERFERENCE & YDSE) Level - II (ADVANCED) Level - II (straight objective Type Questions) Integer Type Questions
1 Video
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
In a Fraunhoffer diffraction experiment at a single slit using light of wavelength 400 nm, the first minimum is formed at an angle of 30∘ Then the direction θ of the first secondary maximum is
View SolutionFrom brewster's law for polarisation, it follows that the angle polarisation depends upon
View SolutionIn the YDSE, the monochromatic source of wavelength λ is placed at a distance d2 from the central axis (as shown in the figure), where d is the separation between the two slits S1andS2 .
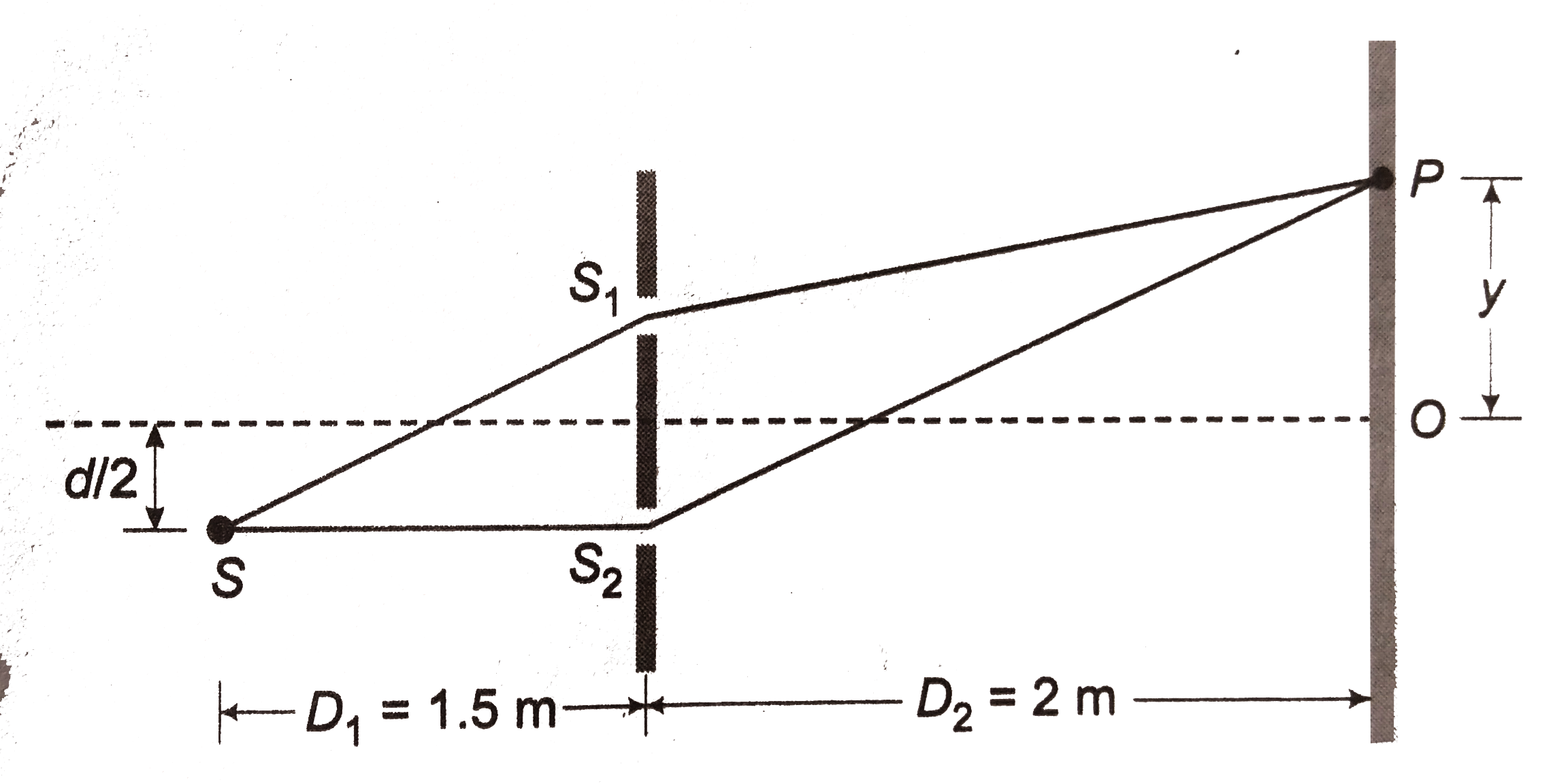
(a)Find the position of the central maxima.
(b) Find the order of interference formed at O.
(c)Now, S is placed on centre dotted line. Find the minimum thickness of the film of refractive indes μ=1.5 to be placed in front of S2 so that intensity at O becomes 34th of the maximum intensity.
(Take λ=6000Å,d=6mm.)
View SolutionA wave is described by the equation y=(1.0mm)sinπ(x2.0cm−t0.01s).
(a) Find time period and wavelength.
(b) Find the speed of particle at x=1.0cm and time t=0.01s.
( c ) What are the speed of the partcle at x=3.0cm, 5.0cmand7.0cm at t=0.01s?
(d) What are the speeds of the partcle at x=1.0cm at t=0.011 , 0.012and0.013s?
View SolutionWhen a train is approaching the stationary observer, the apparent frequency of the whistle observed as 100 Hz, while when it has passed away from the observer with same speed, it is 50 Hz. Calculate the frequency of the whistle when the observer moves with the train V = 330 m/s)
View SolutionThe path difference between two interfering waves at a point on screen is 70.5 tomes the wave length. The point is
View SolutionWaves emitted by two identical sources produces intensity of K unit at a point on screen where path difference between these waves is λ. Calculate the intensity at that point on screen at which path difference is λ4
View SolutionIf two coherent light waves produce minima of fifth order, the path difference between the waves is-
View SolutionThe path of difference between two interfering waves at a point on the screen is λ8 . The ratio of intensity at this point and that at the central fringe will be :
View SolutionThe optical path difference between the two light waves arriving at a point on the screen is
View SolutionThe phase difference between two waves from successive half period zone is
View SolutionIn Young's double slit experiment what is the path difference between the two light waves forming 5th bright band on the screen ?
View SolutionThe path difference between two interfering light waves meeting at a point on the screen is (872)λ. The band obtained at that point is
View SolutionThe path difference between two waves is
View SolutionIf the path difference between the interfering waves is nλ, then the fringes obtained on the screen will be
View SolutionThe average path difference between two waves coming from third and fifth fresnel zones of a wave front at the centre of the screen is
View Solution

