In the above problem, minimum value of t for which the intensity at point P on the screen exactly in front of the upper slit becomes maximum.
0.167s
0.5 s
0.012 s
0.3 s
The correct Answer is:A
To solve the problem regarding the minimum value of time t for which the intensity at point P on the screen exactly in front of the upper slit becomes maximum, we need to analyze the conditions for constructive interference in a double-slit experiment.
1. Understanding the Setup:
- In a double-slit experiment, light waves from two slits interfere with each other. The intensity at a point on the screen depends on the path difference between the two waves reaching that point.
2. Condition for Maximum Intensity:
- For maximum intensity (constructive interference) at point P, the path difference Δx between the two waves must be an integer multiple of the wavelength λ:
Δx=nλ(n=0,1,2,…)
3. Path Difference Calculation:
- The path difference can be expressed in terms of the distance traveled by the light from the slits to point P. If the distance from the slits to point P is d and the angle of incidence is θ, then:
Δx=dsinθ
4. Time Calculation:
- The time t taken for light to travel a distance d is given by:
t=dv
where v is the speed of light.
5. Finding Minimum Time:
- To find the minimum time t for which the intensity at point P becomes maximum, we need to ensure that the path difference corresponds to the first order maximum (i.e., n=1):
dsinθ=λ
- Rearranging gives:
d=λsinθ
- Substituting this into the time equation:
t=λsinθv=λvsinθ
6. Conclusion:
- Therefore, the minimum value of time t for which the intensity at point P becomes maximum is:
t=λvsinθ
- In a double-slit experiment, light waves from two slits interfere with each other. The intensity at a point on the screen depends on the path difference between the two waves reaching that point.
- For maximum intensity (constructive interference) at point P, the path difference Δx between the two waves must be an integer multiple of the wavelength λ:
Δx=nλ(n=0,1,2,…)
- The path difference can be expressed in terms of the distance traveled by the light from the slits to point P. If the distance from the slits to point P is d and the angle of incidence is θ, then:
Δx=dsinθ
- The time t taken for light to travel a distance d is given by:
t=dv
where v is the speed of light.
- To find the minimum time t for which the intensity at point P becomes maximum, we need to ensure that the path difference corresponds to the first order maximum (i.e., n=1):
dsinθ=λ
- Rearranging gives:
d=λsinθ
- Substituting this into the time equation:
t=λsinθv=λvsinθ
- Therefore, the minimum value of time t for which the intensity at point P becomes maximum is:
t=λvsinθ
Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Additional Practice Exercise Level - II (Lecture Sheet (Advanced) More Than One Correct Answer Type Questions
4 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Additional Practice Exercise Level - II (Lecture Sheet (Advanced) Linked Comprehension Type Questions)
2 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Additional Practice Exercise (Level - I) (Main) Straight objective type questions
16 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
The figure shows a schematic diagram showing the arrangement of Youngs's Double Slit Experiment
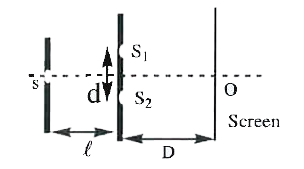
Choose the correct statement (s) related to the wavelength of light used
View SolutionIn Young's double slit experiment the point source is placed slightly off the central axis as shown in figure. The plane of slits (S1,S2) and screen are separated by a distance of 2m. The separation between the slits is 10 mm. The position of the slit above the axis is 1mm. if the wavelength λ=4000Å in the above arrangement

The thickness of the film in the above case is
View SolutionThe phase difference between two waves reaching a point is π2. What is the resultant amplitude. If the individual amplitude are 3 mm and 4mm ?
View SolutionA wave is described by the equation y=(1.0mm)sinπ(x2.0cm−t0.01s).
(a) Find time period and wavelength.
(b) Find the speed of particle at x=1.0cm and time t=0.01s.
( c ) What are the speed of the partcle at x=3.0cm, 5.0cmand7.0cm at t=0.01s?
(d) What are the speeds of the partcle at x=1.0cm at t=0.011 , 0.012and0.013s?
View SolutionWhen a train is approaching the stationary observer, the apparent frequency of the whistle observed as 100 Hz, while when it has passed away from the observer with same speed, it is 50 Hz. Calculate the frequency of the whistle when the observer moves with the train V = 330 m/s)
View SolutionIn Young's double-slit experment, the frist maxima is observed at a fixed point P on the screen. Now, the screen is continously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (center of the screen)
View SolutionIn young's double-slit experiment set up, sources S of wavelength 50 nm illumiantes two slits S_(1) and S_(2) which act as two coherent sources. The sources S oscillates about its own position according to the equation y = 0.5 sin pi t , where y is in nm and t in seconds. The minimum value of time t for which the intensity at point P on the screen exaclty in front of the upper slit becomes minimum is
View SolutionIn a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen. Find the value of n.
View SolutionIn a YDSE using monochromatic visible light, the distance between the plate of slits and the screen is 1.7 m. At point P on the screen which is directly in front of the upper slit, maximum path is observed. Now, the screen is moved 50 cm closer to the plane of slits. Point P now lies between third and fouth minima above the central maxima and the intensity at P in one-fourth of the maxima intensity on the screen. ltbr> Find the wavelength of light if the separation of slits is 2 mm.
View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is lambda and d is the distance between the slits, the angular separation between point P and the center of the screen is
View SolutionThe ratio of intensitics duc to upper and lower slits on the screen of a Young's double-slit experiment is 16:9. Find the ratio of maximum to average intensity on screen.
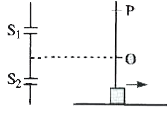
View SolutionIn Young's Double slit experiment, first maxima is observed at a fixed point P on the screen. Now the screen is continuously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (centre of the screen)
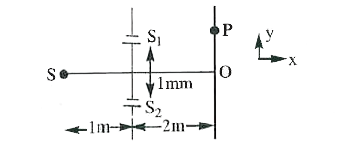
View SolutionIn a Young's double slit experiment set up, source S of wavelength 500 nm illuminates two slit S1 and S2 which act as two coherent sources. The source S oscillates about its won position according to the equation y=0.5sinπt where y is in mm and t in seconds. The minimum value of time t for which the intensity at point P on the screen exactly infront of the upper slit becomes minimum is
View SolutionIn the above problem, minimum value of t for which the intensity at point P on the screen exactly in front of the upper slit becomes maximum.
View SolutionIn Young's double slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is λ and d is the distance between the slits, the angular separation between point P and the centre of the screen is ......
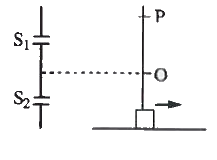
View SolutionIn a young.s Double slit experiment ,first maxima is observed at a fixed point P on the screen Now the screen is continuously moved away from the plane of slits . The ratio of intensity at point P to the intensity at point O (centre of the screen )
View Solution

