Two coherent sources are placed 0.9 mm apart and the fringes are observed one metre away. If it produces the second dark fringe at a distance of 10 mm from the central fringe. The wavelength of monochromatic light is x×10−4cm, What is the value of x ?
The correct Answer is:6
To solve the problem step by step, we will use the formula for the position of dark fringes in an interference pattern created by two coherent sources.
Step 1: Understand the given parameters
- Distance between the two coherent sources (d) = 0.9 mm = 0.9 x 10^(-3) m
- Distance from the sources to the screen (D) = 1 m
- Distance of the second dark fringe from the central maximum (L) = 10 mm = 10 x 10^(-3) m
- We need to find the wavelength of the monochromatic light in the form x x 10^(-4) cm.
Step 2: Identify the formula for dark fringes
The position of the nth dark fringe in a double-slit interference pattern is given by the formula:
L=(2n−1)λD2d
where:
- L = distance of the dark fringe from the central maximum
- n = order of the dark fringe (for the second dark fringe, n = 2)
- λ = wavelength of the light
- D = distance from the sources to the screen
- d = distance between the two coherent sources
Step 3: Substitute the known values into the formula
For the second dark fringe (n = 2):
L=(2⋅2−1)λD2d
This simplifies to:
L=3λD2d
Step 4: Rearrange the formula to solve for the wavelength (λ)
Rearranging gives us:
λ=2dL3D
Step 5: Substitute the values into the equation
Now, substituting the values we have:
- d=0.9×10−3 m
- L=10×10−3 m
- D=1 m
So,
λ=2⋅(0.9×10−3)⋅(10×10−3)3⋅1
λ=2⋅0.9⋅10−63
λ=1.8×10−63
λ=0.6×10−6 m
Step 6: Convert the wavelength to cm
To convert meters to centimeters:
λ=0.6×10−6 m=0.6×10−4 cm
Step 7: Identify the value of x
From the problem statement, we have:
λ=x×10−4 cm
Thus, comparing:
x=0.6
Final Answer
The value of x is 6.
---
- Distance between the two coherent sources (d) = 0.9 mm = 0.9 x 10^(-3) m
- Distance from the sources to the screen (D) = 1 m
- Distance of the second dark fringe from the central maximum (L) = 10 mm = 10 x 10^(-3) m
- We need to find the wavelength of the monochromatic light in the form x x 10^(-4) cm.
The position of the nth dark fringe in a double-slit interference pattern is given by the formula:
L=(2n−1)λD2d
where:
- L = distance of the dark fringe from the central maximum
- n = order of the dark fringe (for the second dark fringe, n = 2)
- λ = wavelength of the light
- D = distance from the sources to the screen
- d = distance between the two coherent sources
For the second dark fringe (n = 2):
L=(2⋅2−1)λD2d
This simplifies to:
L=3λD2d
Rearranging gives us:
λ=2dL3D
Now, substituting the values we have:
- d=0.9×10−3 m
- L=10×10−3 m
- D=1 m
λ=2⋅(0.9×10−3)⋅(10×10−3)3⋅1
λ=2⋅0.9⋅10−63
λ=1.8×10−63
λ=0.6×10−6 m
To convert meters to centimeters:
λ=0.6×10−6 m=0.6×10−4 cm
From the problem statement, we have:
λ=x×10−4 cm
Thus, comparing:
x=0.6
The value of x is 6.
Topper's Solved these Questions
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Additional Practice Exercise (Practice Sheet (Advanced))
6 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - LECTURE SHEET EXERCISE-I (LEVEL -I) (MAIN) straight objective Type Questions
16 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - Additional Practice Exercise Level - II (Lecture Sheet (Advanced) Matrix Matching Type Questions
1 Video
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
- WAVESBOOK - AAKASH SERIESCHAPTER - WAVESEXERCISE - EXERCISE-III (Doppler effect :)
15 Videos
Similar Questions
A slit 5cm wide is irradiated normally with microwaves of wavelength 1cm. Then the angular spread of the central maxima on either side of the incident light is nearly
View SolutionWaves of same amplitude and same frequency from two coherent source overlap at a point. The ratio of the resultant intensity when they arrive in phase to that when they arrive with 90∘ phase difference is
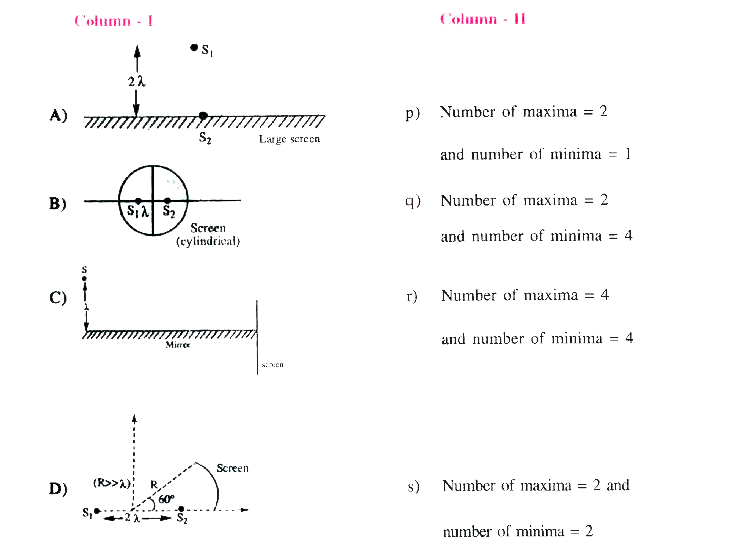
View SolutionS1 and S2 in List I represent coherent point sources, S represents a point source λ = wavelength of light emitted by the sources. Fringe pattern is observed on the screen. Exclude the position of source while detecting the fringe pattern.
View SolutionA wave is described by the equation y=(1.0mm)sinπ(x2.0cm−t0.01s).
(a) Find time period and wavelength.
(b) Find the speed of particle at x=1.0cm and time t=0.01s.
( c ) What are the speed of the partcle at x=3.0cm, 5.0cmand7.0cm at t=0.01s?
(d) What are the speeds of the partcle at x=1.0cm at t=0.011 , 0.012and0.013s?
View SolutionWhen a train is approaching the stationary observer, the apparent frequency of the whistle observed as 100 Hz, while when it has passed away from the observer with same speed, it is 50 Hz. Calculate the frequency of the whistle when the observer moves with the train V = 330 m/s)
View SolutionIn a Young's experiment, two coherent sources are placed 0.90mm apart and the fringes are observed one metre away. If is produces the second dark fringe at a distance of 1mm from the central fringe, the wavelength of monochromatic light used would be
View SolutionIn a Young' s experiment, two coherent sources are placed 0.90 mm apart and the fringes are observed one metre away. If it produces the second dark fringe at a distance of 1 mm from the central fringe, the wvaelength of monochormatic light used would be :
View SolutionIn a Young's double slit experiment, the separation between the two slits is 0.9 mm and the fringes are observed one metre away. If it produces the second dark fringe at a distance of 1 mm from the central fringe, the wavelength of the monochromatic source of light used is
View SolutionTwo coherent sources are placed 0.9 mm apart and the fringes are observed one metre away. The wavelength of monochromatic light used if it produces the second dark fringes at a distance of 10 mm from the central finge will be
View SolutionTwo coherent sources are placed 0.9 mm apart and the fringes are observed one metre away. If it produces the second dark fringe at a distance of 10 mm from the central fringe. The wavelength of monochromatic light is x xx 10^(-4) cm , What is the valye of x ?
View SolutionIn Young's experiment, two coherent sources are placed 0.9 mm apart and fringe are observed one meter away. If it produces second dark fringe at a distance of 1 mm from central fringe, the wavelength of monochromatic light used would ......
View SolutionTwo coherent sources are 0.18mm apart and the fringes are observed on a screen 80 cm away. It is found that with a certain monochromatic source of light, the fourth bright fringe is situated at a distance of 10.8mm from the central fringe. Calculate the wavelength of light.
View SolutionTwo coherent sources are 0.15 mm apart and fringes are observed 1m away with monochromatic light of wavelength 60000. Find
The fringe width in air.
View SolutionTwo coherent sources are placed 0.9 mm apart and the fringes are observed one metre away. The wavelength of monochromatic light used if it produces the second dark fringes at a distance of 10 mm from the central finge will be
View SolutionTwo coherent sources are placed 0.9 mm apart and the fringes are observed one away .If it produces the second dark fringe at a distance of 10 mm from the central fringe . The wavelength of monochromatic light is x×10−4 cm , What is the value of x ?
View SolutionTwo coherent sources are 0.18 mm apart and the fringes are observed on a screen 80cm away. It is found that with a certain monochromatic source of light, the fourth bright fringe is situated at a distance of 10.8 mm from the central fringe. Calculate the wavelength of light.
View Solution

