If vectors →Aand→B are 3ˆi−4ˆj+5ˆk and 2ˆi+3ˆj−4ˆk respectively then the unit vector parallel to →A+→B
To find the unit vector parallel to the sum of vectors →A and →B, we will follow these steps:
Step 1: Define the vectors
Given:
→A=3^i−4^j+5^k
→B=2^i+3^j−4^k
Step 2: Calculate the resultant vector →R
The resultant vector →R is given by:
→R=→A+→B
Substituting the values:
→R=(3^i−4^j+5^k)+(2^i+3^j−4^k)
Step 3: Combine the components
Now, we will combine the components of →R:
→R=(3+2)^i+(−4+3)^j+(5−4)^k
This simplifies to:
→R=5^i−1^j+1^k
Step 4: Find the magnitude of →R
The magnitude of →R is calculated using the formula:
|→R|=√(5)2+(−1)2+(1)2
Calculating this gives:
|→R|=√25+1+1=√27
Step 5: Calculate the unit vector ^u
The unit vector ^u in the direction of →R is given by:
^u=→R|→R|
Substituting the values:
^u=5^i−1^j+1^k√27
Step 6: Final expression for the unit vector
Thus, the unit vector parallel to →A+→B is:
^u=5√27^i−1√27^j+1√27^k
Given:
→A=3^i−4^j+5^k
→B=2^i+3^j−4^k
The resultant vector →R is given by:
→R=→A+→B
Substituting the values:
→R=(3^i−4^j+5^k)+(2^i+3^j−4^k)
Now, we will combine the components of →R:
→R=(3+2)^i+(−4+3)^j+(5−4)^k
This simplifies to:
→R=5^i−1^j+1^k
The magnitude of →R is calculated using the formula:
|→R|=√(5)2+(−1)2+(1)2
Calculating this gives:
|→R|=√25+1+1=√27
The unit vector ^u in the direction of →R is given by:
^u=→R|→R|
Substituting the values:
^u=5^i−1^j+1^k√27
Thus, the unit vector parallel to →A+→B is:
^u=5√27^i−1√27^j+1√27^k
Topper's Solved these Questions
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - SHORT ANSWER TYPE QUESTIONS
10 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
Similar Questions
State parallelogram law of vector addition. Find analytically the magnitude and direction of resultant vector. Apply it to find the resultant when,
(i) Two vectors are parallel to each other
(ii) Two vectors are perpendicular to each other
View SolutionDefine scalar and vector products. Describe them with examples.
View SolutionThe linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
View SolutionA light beam is traveling from Region I to region IV (refer figure). The refractive indices in Region I, II, III, and IV are n0,n0/2,n0/6andn0/8 , respectively. The angle of incidence θ for which the beam just misses entering Region IV is
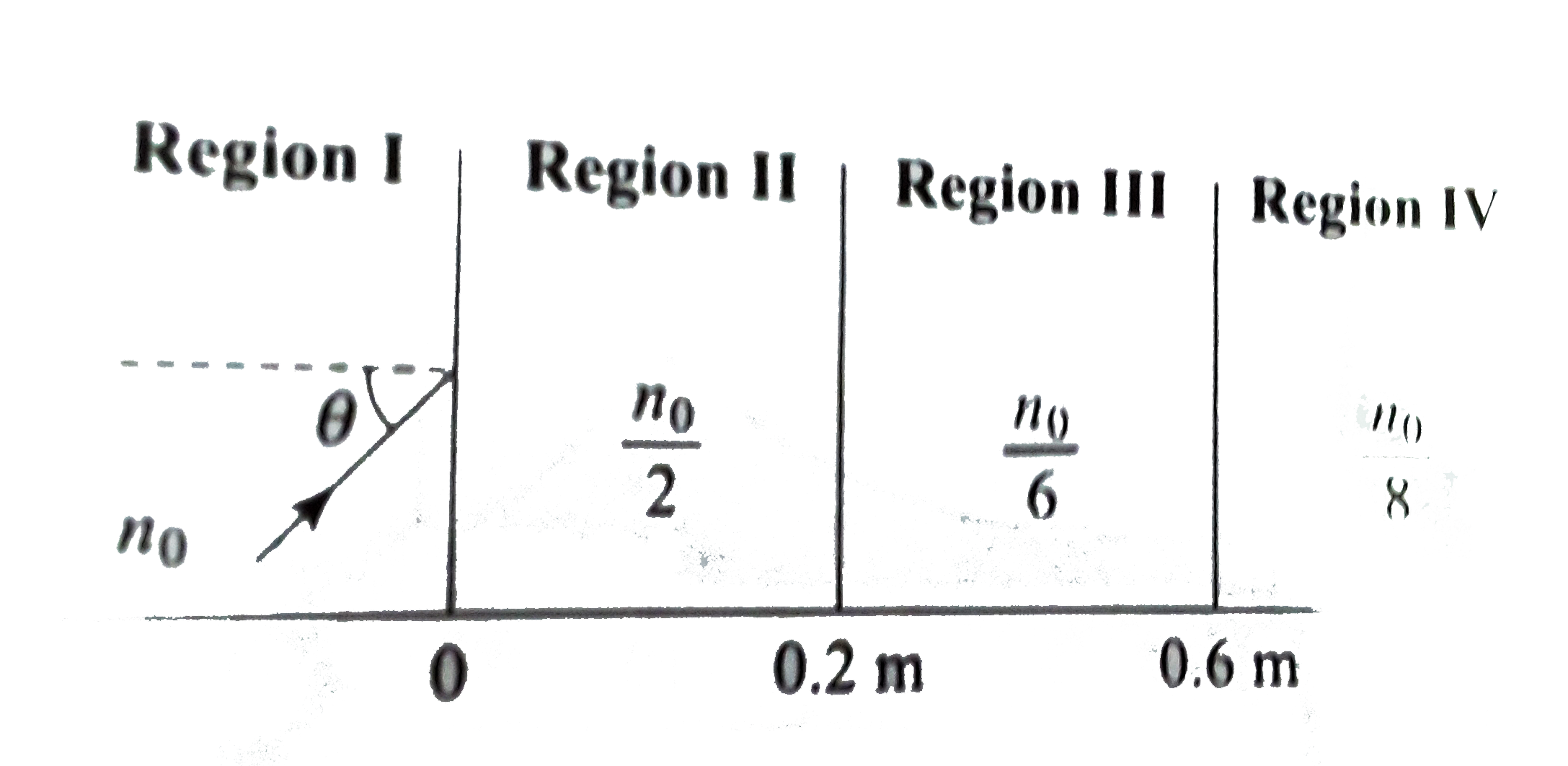
View SolutionIf →a,→b are non-collinear vectors, then
[→a→bˆi]ˆi+[→a→bˆj]ˆj+[→a→bˆk]ˆk=
View SolutionFind the angle between the vectors →a and →b
if |→a|=2∣∣→b∣∣=3 and →a.→b=1
if →a=ˆi+ˆj+ˆk and →b=ˆi−ˆj−ˆk.
View SolutionIf →a=ˆi+ˆj,→b=ˆj+ˆk,→cˆk+ˆi, a unit vector parallel to →a+→b+→c.
View Solutionसदिश →a का सदिश →b की दिशा में प्रक्षेप ज्ञात कीजिए , यदि
(i)→a=ˆi+4ˆj+0ˆk,→b=−ˆi+3ˆk
(ii)→a=2ˆi−ˆj+3ˆk,→b=ˆi+3ˆj+ˆk
(iii)→a=ˆi+ˆj+3ˆk,→b=ˆi−2ˆj+5ˆk
View SolutionIf vecA, vecB are perpendicular vectors :' vecA = 5 hati + 7 hatj - 3 hatk :'vecB = 2 hati + 2 hatj - c hatk . Value of c is
View SolutionThe projection of the vector →a=3ˆi−ˆj−2ˆk on the vector →b=ˆi+2ˆj−3ˆk is :
View SolutionIf →a=ˆi+ˆj−ˆk,→b=−ˆi+2ˆj+2ˆkand→c=−ˆi+2ˆj−ˆk, then a unit vector normal to the vectors →a+→band→b−→c is :
View SolutionIf vectors vecA and vecB are 3 hati - 4 hatj + 5 hatk and 2 hati + 3 hatj - 4hatk respectively then the unit vector parallel to vecA + vecB
View Solution→A=2ˆi+3ˆJ+4ˆk and →B=4ˆi+5ˆj+3ˆk , then the magnitudes of →A−→B…unit
View SolutionFind a unit vector perpendicular to each of the vectors (→a+→b)and(→a−→b) where →a=ˆi+ˆj+ˆk,→b=ˆi+2ˆj+3ˆk
View SolutionFind the angle between the vectors →a and →b
if |→a|=2∣∣→b∣∣=3 and →a.→b=1
if →a=ˆi+ˆj+ˆk and →b=ˆi−ˆj−ˆk.
View SolutionIf →a=ˆi+ˆj,→b=ˆj+ˆk,→cˆk+ˆi, a unit vector parallel to →a+→b+→c.
View Solution

