A man standing still finds rain pouring at angle 30∘ with vertical , when he starts walking forward at a speed of 4Kmph it appears to him that rain pours vertically down. When he runs at triple the speed, what is the angle at which rain appers to pour ?

Case I : When the man is still
VR = actual (absolute )
velocity of rain.
Case : II
When man walks at 4kph.
rain fall vertically
mean horizontal component of
rains. velocity = 4
∴VRsin30∘=4⇒VR=8

Case : III
The man runs at triple the speed VM=12kph.
we have superimposed VM to VR to
get the resultant .
From figure we see tanϕ=O.BOO.=12−4√82−42=8√48=2√3∴ϕ=49
and raindrop makes an angle of 49.6∘ in opposite direction.

टॉपर्स ने हल किए ये सवाल
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - SHORT ANSWER TYPE QUESTIONS
10 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
समान प्रश्न
State parallelogram law of vector addition. Find analytically the magnitude and direction of resultant vector. Apply it to find the resultant when,
(i) Two vectors are parallel to each other
(ii) Two vectors are perpendicular to each other
View SolutionDefine scalar and vector products. Describe them with examples.
View SolutionThe linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
View SolutionA light beam is traveling from Region I to region IV (refer figure). The refractive indices in Region I, II, III, and IV are n0,n0/2,n0/6andn0/8 , respectively. The angle of incidence θ for which the beam just misses entering Region IV is
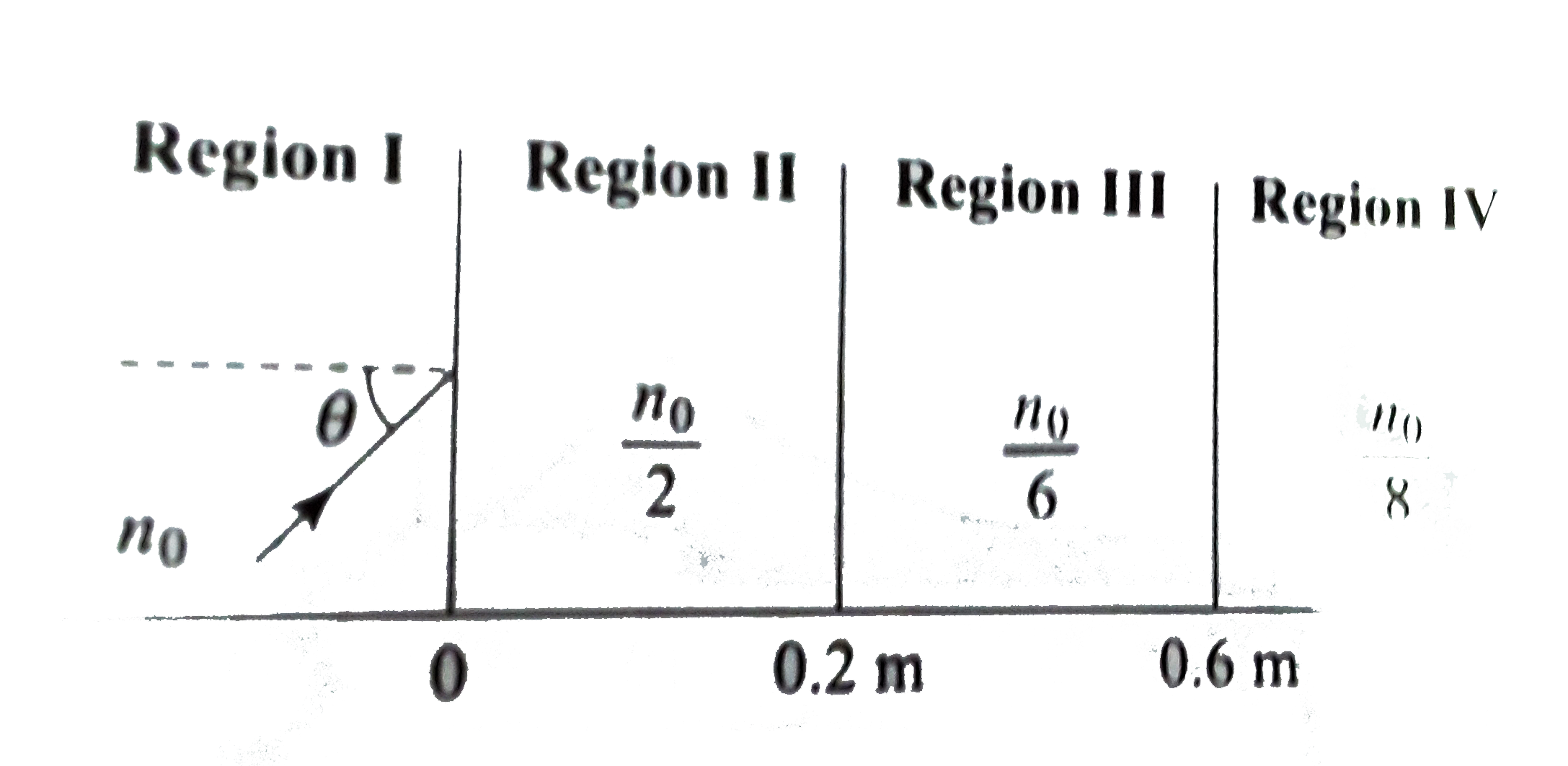
View SolutionTo a man walking at the rate of 3km/h the rain appear to fall vertically downwards. When he increases his speed 6km/h it appears to meet him at an angle of 45∘ with vertical. Find the speed of rain.
View SolutionTo a stationary man, rain appears to be falling at his back at an angle 30∘ with the vertical. As he starts moving forward with a speed of 0.5ms−1, he finds that the rain is falling vertically.
The speed of rain with respect to the stationary man is.
View SolutionTo a stationary man, rain appears to be falling at his back at an angle 30∘ with the vertical. As he starts moving forward with a speed of 0.5ms−1, he finds that the rain is falling vertically.
The speed of rain with respect to the moving man is.
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View SolutionRain, pouring down at an angle alpha with the vertical has a speed of 10ms^(-1) . A girl runs against the rain with a speed of 8ms//^(-1) and sees that the rain makes an angle beta with the vertical, then relation between alpha and beta is
View SolutionTo a man walking at 5kmph rain appears to fall vertically, and when he doubles his speed it appears to make an angle of 30∘ with the vertical. Find the actual velocity of the rain. In what direction will rain appear to fall if the man suddenly turns around when his speed is 5 kmph?
View SolutionA man running at a speed of 5 kmph finds that the rain falls vertically. When he stops running, he finds that the rain is falling at an angle of 60° with the horizontal. The velocity of rain with respect to running man is
View SolutionWhen it is raining vertically down, to a man walking on road the velocity of rain appears to be 1.5 times his velocity. To protect himself from rain he should hold the umbrella at an angle θ to vertical. Then tanθ=
View SolutionA man standing still finds rain pouring at angle 30∘ with vertical , when hs starts walking forward at a speed of 4Kmph it appers to him that rain pours vertically down. When he runs at triple the speed, what is the angle at which rain appers to pour ?

View SolutionRain, pouring down at an angle a with the vertical has a speed of 10 m/s. A girl runs against the rain with a speed of 8 m/s and sees that the rain makes an angle β with the vertical, then relation between αandβ is
View SolutionA man standing still finds rain pouring at an angle 30∘with vertical , when he starts walking forward at a speed of 4 kmph it appears to him that rain pours vertically down . When he runs at riple the speed, what is the angle at which rain appears to pour?
View SolutionTo a man walking at the rate of 3km/h the rain appear to fall vertically downwards. When he increases his speed 6km/h it appears to meet him at an angle of 45∘ with vertically. Find the speed of rain.
View Solution

