if →A→B=→C and A+B=C, then the angle between →A and →B :
tan−1(ba)
Topper's Solved these Questions
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - NUMERICAL EXXERCISE (LEVEL -2)
21 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
12 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
Similar Questions
The width of a river is 3√3 km. A boat has a velocity of √3 km/s and starts to cross the river in a direction perpendicular to the bank of the river. If the river is flowing with a velocity 2km/sec, find the distance drifted by the boat.
View SolutionFind the components of a vector A=2ˆi+3ˆj along the directions of ˆi+ˆjandˆi−ˆj.
View SolutionIf the vectors 2ˆi+2ˆj−ˆkand3ˆi−6ˆj+nˆk are mutually perpendicular, find the value of n ?
View SolutionThe linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
View SolutionA light beam is traveling from Region I to region IV (refer figure). The refractive indices in Region I, II, III, and IV are n0,n0/2,n0/6andn0/8 , respectively. The angle of incidence θ for which the beam just misses entering Region IV is
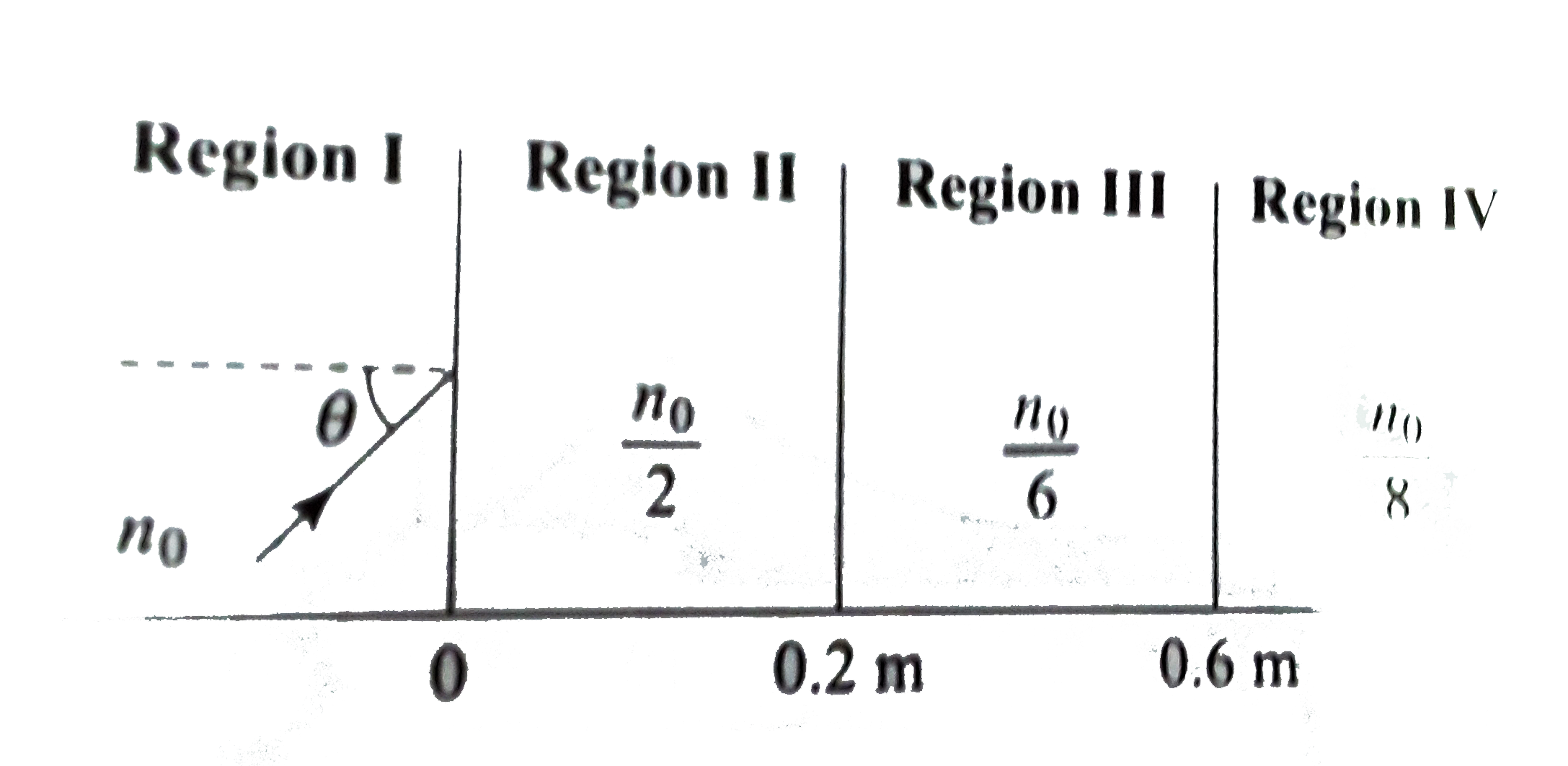
View SolutionIf →a,→b,→c are unit vectors such that veca is perpendicular to →band→cand∣∣→a+→b+→c∣∣=1 then the angle between →band→c is (A) π2(B)pi(C)0(D)(2pi)/3
View Solution→A,→Band→C are vectors such that →C=→A+→Band→C⊥→A and also C= A . Angle between →Aand→B is :
View SolutionIf →A+→B=→CandA+B+C=0, then the angle between →Aand→B is :
View SolutionIf →a,→b,→c are unit vectors such that →a is perpendicular to the plane of →b,→c and the angle between →b,→c is π3, then ∣∣→a+→b+→c∣∣=
View SolutionIf veca+vecb=vecc and a+b=c , find the angle between veca and vecb .
View SolutionIf →a+→b=→c, and a+b=c then the angle between →aand→b is
View Solutionदिया है →A+→B=→C तथा →C,→A के लम्बवत है इसके अतिरिक्त यदि ∣∣→A∣∣=∣∣→C∣∣, तो →A तथा →B के बीच कोण होगा
View Solutionयदि →a+→b=→c तथा a+b=c, तब →a तथा →b के मध्य कोण होगा
View SolutionAngle between →Aand→B is θ1 and angle between →Aand→C be θ2.If →A⋅→B=→A⋅→C, then →B=→C.
View Solutionयदि →A+→B=→C तथा A+B=C है →A व →B के मध्य कोण है
View SolutionIf veca,vecb"and"vecc are three vectors such that veca+vecb=vecc and further a^(2)+b^(2)=c^(2) , find the angle between them veca"and"vecb ?
View Solution

