IF ¯¯¯P+¯¯¯Q=¯¯¯RandP=Q=R√2 then find the angles between the pairs of vectors (¯¯¯P,¯¯¯Q),(¯¯¯Q,¯¯¯R)and(¯¯¯R,¯¯¯P) respectively
To solve the problem, we need to find the angles between the pairs of vectors ¯P,¯Q,¯R given that ¯P+¯Q=¯R and P=Q=R√2.
Step 1: Understand the given equations
From the problem, we have:
1. ¯P+¯Q=¯R
2. P=Q=R√2
Step 2: Substitute the values of P and Q
Since P=Q=R√2, we can write:
¯P=¯R√2and¯Q=¯R√2
Step 3: Substitute into the vector equation
Substituting ¯P and ¯Q into the equation ¯P+¯Q=¯R:
¯R√2+¯R√2=¯R
This simplifies to:
2¯R√2=¯R
This means:
√2⋅¯R=¯R
This is consistent, confirming our substitutions.
Step 4: Find the angles between the vectors
1. Angle between ¯P and ¯Q:
Since ¯P and ¯Q are equal in magnitude and are the same vector scaled by 1√2, the angle between them can be found using the cosine rule:
cosθPQ=¯P⋅¯Q|¯P||¯Q|
Since ¯P+¯Q=¯R forms a right triangle, the angle θPQ=90∘.
2. Angle between ¯Q and ¯R:
We can find this angle using the fact that ¯R=¯P+¯Q. The triangle formed is an isosceles right triangle, which gives:
θQR=45∘
3. Angle between ¯R and ¯P:
By symmetry, since ¯P and ¯Q are equal and the triangle is isosceles, the angle θRP is also:
θRP=45∘
Final Answer
Thus, the angles between the pairs of vectors are:
- Angle between ¯P and ¯Q = 90∘
- Angle between ¯Q and ¯R = 45∘
- Angle between ¯R and ¯P = 45∘
From the problem, we have:
1. ¯P+¯Q=¯R
2. P=Q=R√2
Since P=Q=R√2, we can write:
¯P=¯R√2and¯Q=¯R√2
Substituting ¯P and ¯Q into the equation ¯P+¯Q=¯R:
¯R√2+¯R√2=¯R
This simplifies to:
2¯R√2=¯R
This means:
√2⋅¯R=¯R
This is consistent, confirming our substitutions.
1. Angle between ¯P and ¯Q:
Since ¯P and ¯Q are equal in magnitude and are the same vector scaled by 1√2, the angle between them can be found using the cosine rule:
cosθPQ=¯P⋅¯Q|¯P||¯Q|
Since ¯P+¯Q=¯R forms a right triangle, the angle θPQ=90∘.
We can find this angle using the fact that ¯R=¯P+¯Q. The triangle formed is an isosceles right triangle, which gives:
θQR=45∘
By symmetry, since ¯P and ¯Q are equal and the triangle is isosceles, the angle θRP is also:
θRP=45∘
Thus, the angles between the pairs of vectors are:
- Angle between ¯P and ¯Q = 90∘
- Angle between ¯Q and ¯R = 45∘
- Angle between ¯R and ¯P = 45∘
Topper's Solved these Questions
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - NUMERICAL EXXERCISE (LEVEL -1)
13 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
Similar Questions
Find the components of a vector A=2ˆi+3ˆj along the directions of ˆi+ˆjandˆi−ˆj.
View SolutionA particle of mass 3kg. moves under the force of 4ˆi+8ˆj+10ˆkN. If the particle starts from rest and was at origin initially. Its new co-ordinates after 3 second is:-
View SolutionThe linear charge density on a dielectric ring of radius R vanes with θ as λ=λ0cosθ/2, where λ0 is constant. Find the potential at the center O of the ring [in volt].
View SolutionA light beam is traveling from Region I to region IV (refer figure). The refractive indices in Region I, II, III, and IV are n0,n0/2,n0/6andn0/8 , respectively. The angle of incidence θ for which the beam just misses entering Region IV is
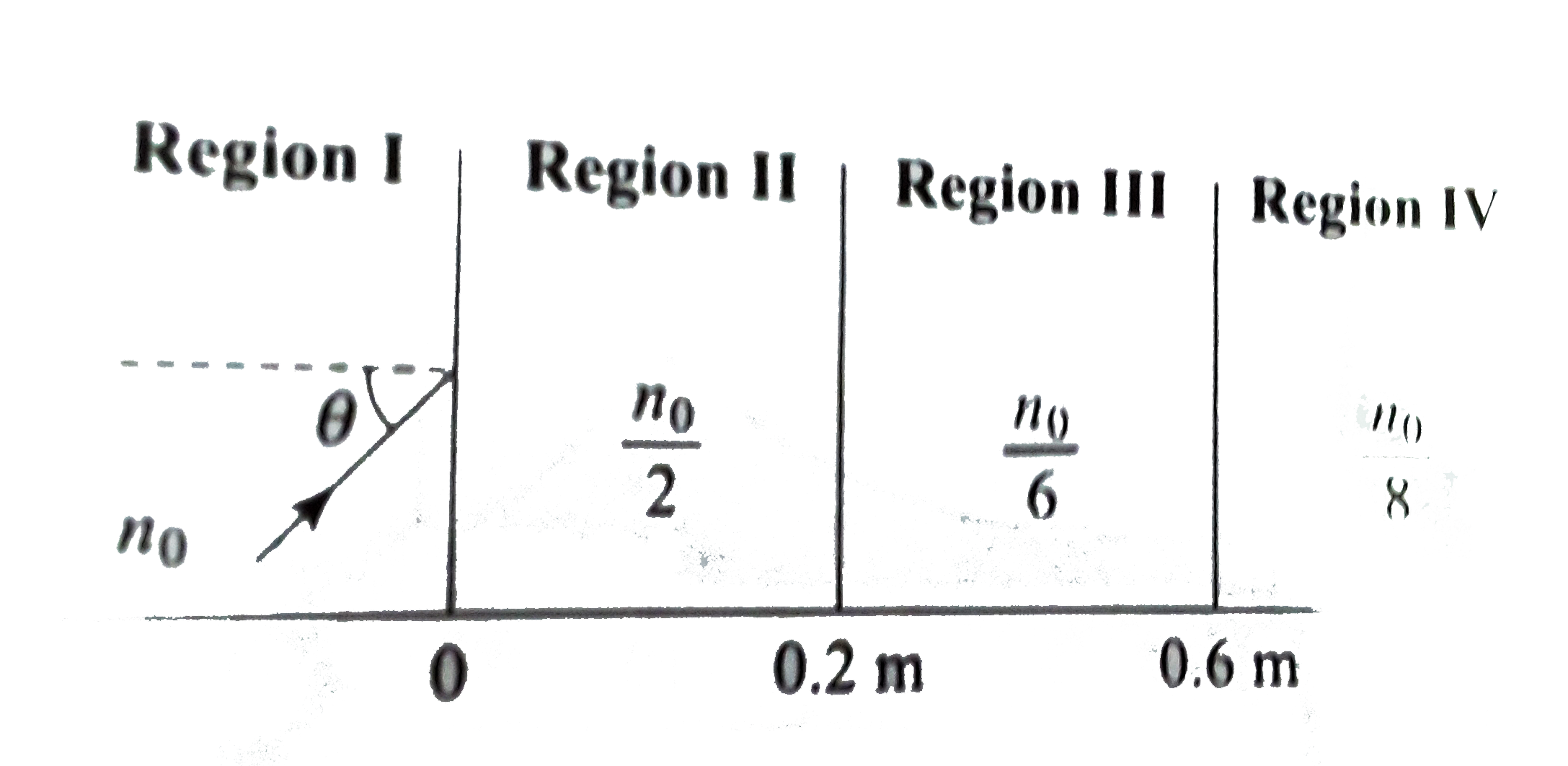
View SolutionIf ¯a,¯b,¯c are non-coplaner vectors and
¯p=¯bׯc[¯b¯c¯a],¯q=¯cׯa[¯c¯a¯b],¯r=¯aׯb[¯a¯b¯c],then :
(¯b+¯c).¯p+(¯c+¯a).¯q+(¯a+¯b).¯r=
View SolutionI is the incentre of ΔABC.
Forces ¯¯¯P,¯¯¯Q,¯¯¯R acting along IA,IB,IC respectively are in equilibrium. Then ∣∣¯¯¯P∣∣:∣∣¯¯¯Q∣∣:∣∣¯¯¯R∣∣=
View SolutionIf ¯a=2¯p+3¯q−¯r,¯b=¯p−2¯q+2¯rand¯c=−2¯p+¯q−2¯rand¯¯¯R=3¯p−¯q+2¯r, where ¯p,¯q,¯r are non-coplanar vectors, then ¯¯¯R in terms of ¯a,¯b,¯c is
View SolutionIf ¯p=¯bׯc¯a ¯b ¯c,¯q=¯cׯa¯a ¯b ¯c,¯r=¯aׯb¯a ¯b ¯c, where ¯a,¯b,¯c are three non-coplanar vectors, then the value of (¯a+¯b+¯c).(¯p+¯q+¯r) is given by
View SolutionIf ¯a,¯b,¯c are three non-coplanar vectors and ¯p,¯q,¯r are defined by the relations ¯p=¯bׯc¯a¯b¯c,¯q=¯cׯa¯a¯b¯c,¯r=¯aׯb¯a¯b¯c then (¯a+¯b).¯p+(¯b+¯c).¯q+(¯c+¯a).¯r=
View SolutionThe equation of line is ¯r=¯p+t(¯q−¯p), where P(¯p)≡(3,4,1)andQ(¯q)≡(5,1,6). The value of t for which the line crosses XY - plane is
View SolutionLet ¯a,¯b,¯c be three coplanar unit vectors such that ¯a+¯b+¯c=¯c. If three vectors ¯p,¯q,¯r parallel to ¯a,¯b,¯c respectively and having integral but different magnitudes , then among the following options |¯p+¯q+¯r| can take a value equal to
View SolutionIf ¯p+¯q+¯r=¯0,|¯p|=3,|¯q|=5,|¯r|=7 . Then angle between ¯pand¯q is
View SolutionIF barP + barQ = barR and P=Q = (R )/(sqrt(2)) then find the angles between the pairs of vectors ( barP , barQ ) , ( barQ,barR) and ( barR, barP) respectively
View SolutionIf →a,→b,→c are three coplanar vectors, ¯p,¯q,¯r are non-zero vectors then ∣∣ ∣ ∣∣¯p⋅¯a¯p⋅¯b¯p⋅¯c¯q⋅¯a¯q⋅¯b¯q⋅¯c¯r⋅¯a¯r⋅¯b¯r⋅¯c∣∣ ∣ ∣∣=
View SolutionIf ¯p=(2,1,3),¯q=(−2,3,1),¯r=(3,−2,4)and¯j is the unit vector in the direction of Y -axis, then (2¯p+3¯q−4¯r).¯j=
View SolutionIf ¯p=(3,−1,5),¯q=(1,2,−3). A vector ¯r is such that it is perpendicular to Z-axis and satisfies the conditions ¯r.¯p=9
¯r.¯q=−4, then ¯r =
View Solution

