To increase the frequency by 20 %, the tension in the string vibrating on a sonometer has to be increased by
0.44
0.33
0.22
0.11
The correct Answer is:A
To solve the problem of how much the tension in the string must be increased to achieve a 20% increase in frequency, we can follow these steps:
1. Understand the relationship between frequency and tension:
The frequency F of a vibrating string is related to the tension T in the string by the formula:
F∝√T
This means that if the tension increases, the frequency also increases.
2. Define initial conditions:
Let's assume the initial frequency F1 is 100 Hz. To find the new frequency F2 after a 20% increase:
F2=F1+0.2×F1=100+20=120 Hz
3. Set up the ratio of frequencies:
Using the relationship between frequency and tension, we can write:
F2F1=√T2√T1
Substituting the known frequencies:
120100=√T2√T1
This simplifies to:
65=√T2√T1
4. Square both sides:
Squaring both sides to eliminate the square root gives:
(65)2=T2T1
This results in:
3625=T2T1
5. Express T2 in terms of T1:
If we let T1=100 (for simplicity), we can express T2:
T2=T1×3625=100×3625=144
6. Calculate the increase in tension:
The increase in tension x is:
x=T2−T1=144−100=44
7. Calculate the percentage increase in tension:
To find the percentage increase in tension:
Percentage increase=xT1×100=44100×100=44%
In decimal form, this is:
0.44
Conclusion:
The tension in the string must be increased by 0.44 (or 44%) to achieve a 20% increase in frequency.
The frequency F of a vibrating string is related to the tension T in the string by the formula:
F∝√T
This means that if the tension increases, the frequency also increases.
Let's assume the initial frequency F1 is 100 Hz. To find the new frequency F2 after a 20% increase:
F2=F1+0.2×F1=100+20=120 Hz
Using the relationship between frequency and tension, we can write:
F2F1=√T2√T1
Substituting the known frequencies:
120100=√T2√T1
This simplifies to:
65=√T2√T1
Squaring both sides to eliminate the square root gives:
(65)2=T2T1
This results in:
3625=T2T1
If we let T1=100 (for simplicity), we can express T2:
T2=T1×3625=100×3625=144
The increase in tension x is:
x=T2−T1=144−100=44
To find the percentage increase in tension:
Percentage increase=xT1×100=44100×100=44%
In decimal form, this is:
0.44
The tension in the string must be increased by 0.44 (or 44%) to achieve a 20% increase in frequency.
Topper's Solved these Questions
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-III (LEVEL-II(ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
7 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-III (LEVEL-II(ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
3 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - LECTURE SHEET (EXERCISE-II (LEVEL-II(ADVANCED) INTEGER TYPE QUESTIONS))
3 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
Similar Questions
A pulse shown here is reflected from the rigid wall A and then from free end B. The shape of the string after these 2 reflection will be
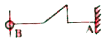
View SolutionStanding waves can be produced.
View SolutionA loop of a string of mass length μ and redius R is rotated about an axis passing through centre perpendicular to the plane with an angular velocity ω.A small disturbance is created in the loop having the same sense of rotation. The linear speed of the disturbance observer is
View SolutionThe length of a rectangular plate is measured as 10 cm by a vernier scale of least count 0.01 cm and its breadth as 5 cm by the same scale. The percentage error in area is
View SolutionA wave is described by the equation y=(1.0mm)sinπ(x2.0cm−t0.01s).
(a) Find time period and wavelength.
(b) Find the speed of particle at x=1.0cm and time t=0.01s.
( c ) What are the speed of the partcle at x=3.0cm, 5.0cmand7.0cm at t=0.01s?
(d) What are the speeds of the partcle at x=1.0cm at t=0.011 , 0.012and0.013s?
View SolutionA tuning fork of frequency 512 Hz is vibrated with sonometer wire and 6 beats per seconds are heard. The beat frequency reduces if the tension in the string is slightly increased. The original freqency of vibration of the string is
View SolutionThe fundamental frequency of a sonometer wire increases by 6Hz if its tension is increased by 44% keeping the length constant. Find the change in the fundamental frequency of the sonometer when the length of the wire is increased by 20% keeping the original tension in the wire.
View SolutionTo increase the frequency by 20% , the tension in the string vibrating on a sonometer has to be increased by
View SolutionThe fundamental frequency of a sonometer wire increases by 5Hz, if the tension is increased by 21% . The fundamental frequency of the sonometer wire is a Hz is
View Solutionएक तनी हुई डोरी के तनाव में 69% की वृद्धि कर दी जाती है। कम्पन की आवृत्ति नियत बनाये रखने के लिए इसकी लम्बाई में कितने प्रतिशत की वृद्धि करनी चाहिए
View SolutionA tuning fork of frequency 512 Hz is vibrated with sonometer wire and 6 beats per seconds are heard. The beat frequency reduces if the tension in the string is slightly increased. The original frequency of vibration of the string is
View SolutionTo increase the frequency by 20 %, the tension in the string vibrating on a sonometer has to be increased by
View SolutionWhen the tension in a string is increased by 44%. the frequency increased by 10Hz the frequency of the string is
View SolutionTo increase the frequency by 20 %, the tension in the string vibrating on a sonometer has to be increased by
View SolutionIf tension is increased by 4% in vibrating string find % change in speed of wave?
View SolutionA tuning fork of frequency 512 Hz is vibrated with a sonometer wire and 6 beats per second are heard. The beat frequency reduces if the tension is the string is slightly increased . The original frequency of vibration of the string is
View Solution

