The ratio of densities of nitrogen and oxygen is 14 : 16. The temperature at which the speed of sound in nitrogen will be same as that in oxygen at 55∘C is
35∘C
48∘C
65∘C
14∘C
The correct Answer is:D
To solve the problem, we need to find the temperature at which the speed of sound in nitrogen will be the same as that in oxygen at 55°C. We know the ratio of the densities of nitrogen and oxygen is given as 14:16.
1. Understand the relationship between density and molecular mass:
The ratio of densities of two gases is equal to the ratio of their molecular masses. Therefore, we can express this as:
Density of NitrogenDensity of Oxygen=Molecular Mass of NitrogenMolecular Mass of Oxygen=1416
2. Use the formula for the speed of sound in a gas:
The speed of sound v in a gas is given by the formula:
v=√γRTM
where γ is the adiabatic index, R is the gas constant, T is the temperature in Kelvin, and M is the molecular mass of the gas.
3. Set up the equation for both gases:
Let TN2 be the temperature of nitrogen and TO2 be the temperature of oxygen (which is 55°C or 328 K). We can write the equations for the speed of sound in nitrogen and oxygen:
vN2=√γRTN2MN2
vO2=√γRTO2MO2
4. Set the speeds equal to each other:
Since we want the speeds to be equal:
√γRTN2MN2=√γRTO2MO2
Squaring both sides and canceling out common terms gives:
TN2MN2=TO2MO2
5. Substituting known values:
Rearranging the equation gives:
TN2=TO2⋅MN2MO2
We know TO2=55°C=328K and the ratio of molecular masses from the density ratio:
MN2MO2=1416=78
Now substituting these values:
TN2=328K⋅78
6. Calculating TN2:
TN2=328K⋅0.875=287K
7. Convert Kelvin to Celsius:
To convert Kelvin back to Celsius:
TN2=287K−273=14°C
Final Answer:
The temperature at which the speed of sound in nitrogen will be the same as that in oxygen at 55°C is 14°C.
The ratio of densities of two gases is equal to the ratio of their molecular masses. Therefore, we can express this as:
Density of NitrogenDensity of Oxygen=Molecular Mass of NitrogenMolecular Mass of Oxygen=1416
The speed of sound v in a gas is given by the formula:
v=√γRTM
where γ is the adiabatic index, R is the gas constant, T is the temperature in Kelvin, and M is the molecular mass of the gas.
Let TN2 be the temperature of nitrogen and TO2 be the temperature of oxygen (which is 55°C or 328 K). We can write the equations for the speed of sound in nitrogen and oxygen:
vN2=√γRTN2MN2
vO2=√γRTO2MO2
Since we want the speeds to be equal:
√γRTN2MN2=√γRTO2MO2
Squaring both sides and canceling out common terms gives:
TN2MN2=TO2MO2
Rearranging the equation gives:
TN2=TO2⋅MN2MO2
We know TO2=55°C=328K and the ratio of molecular masses from the density ratio:
MN2MO2=1416=78
Now substituting these values:
TN2=328K⋅78
TN2=328K⋅0.875=287K
To convert Kelvin back to Celsius:
TN2=287K−273=14°C
The temperature at which the speed of sound in nitrogen will be the same as that in oxygen at 55°C is 14°C.
Topper's Solved these Questions
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-II (LEVEL-II(ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
4 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-II (LEVEL-II(ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS))
4 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SET (EXERCISE-II (LEVEL-I(MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS))
4 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - II)
97 Videos
Similar Questions
The figure shows a snap photograph of a vibrating string at t=0. The particle P is observed moving up with velocity 20√3cm/s. The tangent at P makes an angle 60∘ with x-axis.
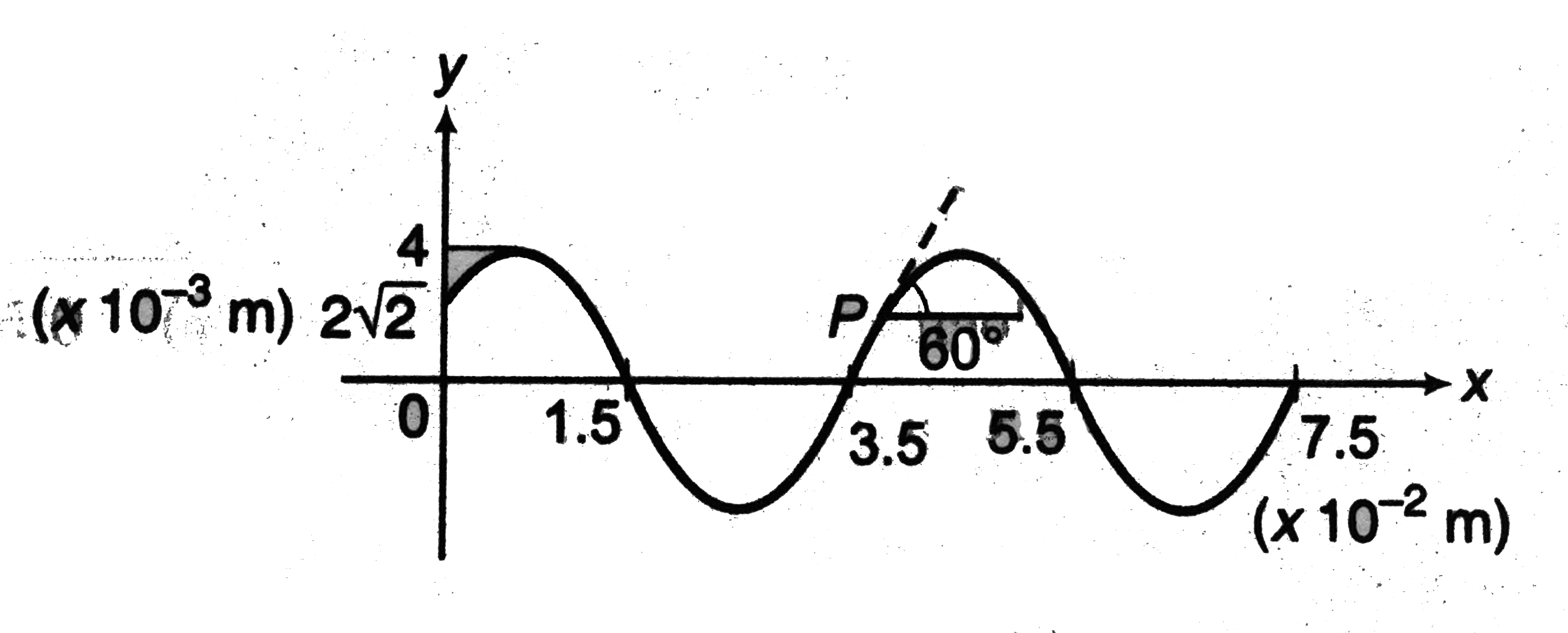
(a) Find the direction in which the wave is moving.
(b) Write the equation of the wave.
(c) The total energy carries by the wave per cycle of the string. Assuming that the mass per unit length of the string is 50g/m.
View SolutionOne end of a 60m long rope of mass 1.8 kg is tied to a rigid horizontal support held high above the ground. The rope hangs vertically and kept taut by a weight 'W' suspended at its lower end. A person jerks the lower end of the rope sideways in a sinusoidal manner and a transverse wave of frequency 2 Hz and amplitude 10cm passes along the rope such that there are 2 cycles of the wave in the total length of the rope. Neglecting the weight of the rope as compared to the suspended weight W and with g = 10m/s2, answer the following questions. (S=75×10−4m2)

In the questions above, weight of the rope has been neglected as compared to the suspended weight. However, if we also account for the weight of the rope. the speed of the wave at the top of the rope will be
View SolutionA transverse wave propagating on a stretched string of linear density 3×10−4kg−m−1 is represented by the equation
y=0.2sin(1.5x+60t)
Where x is in metre and t is in second. The tension in the string (in Newton) is
View SolutionThe length of a rectangular plate is measured as 10 cm by a vernier scale of least count 0.01 cm and its breadth as 5 cm by the same scale. The percentage error in area is
View SolutionA wave is described by the equation y=(1.0mm)sinπ(x2.0cm−t0.01s).
(a) Find time period and wavelength.
(b) Find the speed of particle at x=1.0cm and time t=0.01s.
( c ) What are the speed of the partcle at x=3.0cm, 5.0cmand7.0cm at t=0.01s?
(d) What are the speeds of the partcle at x=1.0cm at t=0.011 , 0.012and0.013s?
View SolutionThe ratio of densities of oxygen and nitrogen is 16:14. At what temperature, the speed of sound in oxygen will be equal to its sped in nitrogen at 14∘C?
View SolutionAt what temperature, velocity of sound in oxygen is same as that in nitrogen at 10∘C? Given their densities at 0∘C are in the ratio 16:4.
View Solutionकिस ताप पर ऑक्सीजन में ध्वनि की चाल वही होगी जो की 14∘C पर नाइट्रोजन में है। ऑक्सिकन व नाइट्रोजन के अणुभार क्रमशः 32 व 48 है।
View Solutionकिसी ताप पर ऑक्सीजन में ध्वनि की चाल वही होगी जो की 28∘C पर नाइट्रोजन में है? ऑक्सीजन व नाइट्रोजन के अणुभार क्रमशः 32 व 28 है।
View Solutionकिस ताप पर ध्वनि की हाइड्रोजन में वही चाल होगी जो कि 100∘C पर आँक्सीजन में है? ऑक्सीजन व हाइड्रोजन के घनत्व 16:1 के अनुपात में होते हैं।
View Solution0∘C और 760 mm दाब पर ऑक्सीजन का घनत्व 16 और नाइट्रोजन का घनत्व 14 है। किस ताप पर ऑक्सीजन का घनत्व उतना ही हो जाएगा जितना कि 0∘C पर नाइट्रोजन का है जबकि दाब स्थिरांक है?
View Solutionऑक्सीजन व नाइट्रोजन के घनत्वों में अनुपात 16:14 है ऑक्सीजन में किस ताप पर ध्वनि का वह वेग होगा , जो नाइट्रोजन में 15∘C पर है ?
View Solutionऑक्सीजन व नाइट्रोजन के घनत्वों का अनुपात 16:14 है। किस ताप पर ऑक्सीजन में ध्वनि की चाल वही होगी जो 14∘Cपर नाइट्रोजन में है ?
View SolutionAt what temperature is the velocity of sound in nitrogen equal to its velocity in oxygen at 20^(@) C? The atomic weights of oxygen and nitrogen are in the ratio 16 :14
View SolutionThe ratio of the densities of oxygen and nitrogen is 16 : 14 . Calculate the temperature when the speed of sound in nitrogen gas at 17^(@) C is equal to the speed of sound in oxygen gas .
View SolutionFind the temperature at which speed of sound in nitrogen is equal to speed of sound in chlorine at 20^(@)C . The densities of nitrogen and chlorine are in ratio 14 : 35.
View Solution

