The string of a sonometer is divided into two parts with the help of a wedge. The total length of the string is 1 m and the two parts differ by 2mm. When sounded together they produced two beats per second. The frequencies of the notes emitted by the two parts are
499 & 497 Hz
501 & 499 Hz
501 & 503 Hz
none
The correct Answer is:B
To solve the problem, we need to find the frequencies of the two parts of the string when it is divided by a wedge. Here’s a step-by-step solution:
Step 1: Define the lengths of the two parts of the string
Let:
- L1 = length of the first part of the string
- L2 = length of the second part of the string
According to the problem, the total length of the string is given as:
L1+L2=1m
Converting this to centimeters:
L1+L2=100cm(Equation 1)
Step 2: Set up the difference in lengths
The problem states that the two parts differ by 2 mm. Converting this to centimeters gives:
L1−L2=0.2cm(Equation 2)
Step 3: Solve the system of equations
Now, we can solve the two equations simultaneously. Adding Equation 1 and Equation 2:
(L1+L2)+(L1−L2)=100+0.2
This simplifies to:
2L1=100.2cm
Thus, we find:
L1=100.22=50.1cm
Now, substituting L1 back into Equation 1 to find L2:
L2=100−L1=100−50.1=49.9cm
Step 4: Convert lengths to meters
Convert L1 and L2 to meters:
L1=0.501m,L2=0.499m
Step 5: Use the frequency formula
The frequency of a vibrating string is given by the formula:
F=VL
where V is the velocity of the wave on the string.
Step 6: Set up the beat frequency equation
The problem states that the two parts produce 2 beats per second. The beat frequency ΔF is given by:
ΔF=|F1−F2|=2Hz
Substituting the frequencies:
∣∣∣VL1−VL2∣∣∣=2
Step 7: Substitute the lengths
Substituting L1 and L2:
∣∣∣V0.501−V0.499∣∣∣=2
Factoring out V:
V(10.501−10.499)=2
Step 8: Calculate the velocity
Calculating the difference:
10.501−10.499=0.499−0.5010.501×0.499=−0.0020.249999499≈−0.008
Thus:
V×(−0.008)=2⟹V≈20.008=250m/s
Step 9: Calculate the frequencies
Now, substituting V back to find F1 and F2:
F1=2500.501≈499Hz
F2=2500.499≈501Hz
Final Answer
The frequencies of the notes emitted by the two parts are:
- F1≈499Hz
- F2≈501Hz
Let:
- L1 = length of the first part of the string
- L2 = length of the second part of the string
L1+L2=1m
Converting this to centimeters:
L1+L2=100cm(Equation 1)
The problem states that the two parts differ by 2 mm. Converting this to centimeters gives:
L1−L2=0.2cm(Equation 2)
Now, we can solve the two equations simultaneously. Adding Equation 1 and Equation 2:
(L1+L2)+(L1−L2)=100+0.2
This simplifies to:
2L1=100.2cm
Thus, we find:
L1=100.22=50.1cm
L2=100−L1=100−50.1=49.9cm
Convert L1 and L2 to meters:
L1=0.501m,L2=0.499m
The frequency of a vibrating string is given by the formula:
F=VL
where V is the velocity of the wave on the string.
The problem states that the two parts produce 2 beats per second. The beat frequency ΔF is given by:
ΔF=|F1−F2|=2Hz
Substituting the frequencies:
∣∣∣VL1−VL2∣∣∣=2
Substituting L1 and L2:
∣∣∣V0.501−V0.499∣∣∣=2
Factoring out V:
V(10.501−10.499)=2
Calculating the difference:
10.501−10.499=0.499−0.5010.501×0.499=−0.0020.249999499≈−0.008
Thus:
V×(−0.008)=2⟹V≈20.008=250m/s
Now, substituting V back to find F1 and F2:
F1=2500.501≈499Hz
F2=2500.499≈501Hz
The frequencies of the notes emitted by the two parts are:
- F1≈499Hz
- F2≈501Hz
Topper's Solved these Questions
- WAVE MOTIONBook:AAKASH SERIESChapter:WAVE MOTIONExercise:PRACTICE SET (EXERCISE-V (LEVEL-II(ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
Explore 11 Videos
- WAVE MOTIONBook:AAKASH SERIESChapter:WAVE MOTIONExercise:PRACTICE SET (EXERCISE-V (LEVEL-II(ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS))
Explore 2 Videos
- WAVE MOTIONBook:AAKASH SERIESChapter:WAVE MOTIONExercise:PRACTICE SET (EXERCISE-II (LEVEL-II(ADVANCED) MATRIX MATCHING TYPE QUESTIONS))
Explore 1 Video
- UNITS AND MEASUREMENTSBook:AAKASH SERIESChapter:UNITS AND MEASUREMENTSExercise:EXERCISE -3
Explore 66 Videos
- WAVE MOTION AND SOUNDBook:AAKASH SERIESChapter:WAVE MOTION AND SOUNDExercise:PROBLEMS (LEVEL - II)
Explore 97 Videos
Similar Questions
In a closed end pipe of length 105cm , standing waves are set up corresponding to the third overtone . What distance from the closed end, amongst the following is a pressure node?
View SolutionFour open organ popes of different length and different gases at same temperature as shown in figure. Let fA,fB,fC and fD be their fundamental frequencies then : [Take γCO2=43]
_E01_065_Q01.png) .
.
View SolutionA wave disturbance in a medium is described by Y=0.02cos(50πt+π2)cosπx . Where x and y are in m and t in sec. The values in Column-II are in SI units.
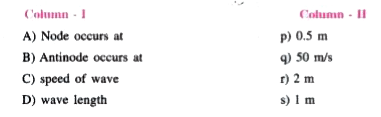
View SolutionThe length of a rectangular plate is measured as 10 cm by a vernier scale of least count 0.01 cm and its breadth as 5 cm by the same scale. The percentage error in area is
View SolutionA wave is described by the equation y=(1.0mm)sinπ(x2.0cm−t0.01s).
(a) Find time period and wavelength.
(b) Find the speed of particle at x=1.0cm and time t=0.01s.
( c ) What are the speed of the partcle at x=3.0cm, 5.0cmand7.0cm at t=0.01s?
(d) What are the speeds of the partcle at x=1.0cm at t=0.011 , 0.012and0.013s?
View SolutionThe two parts of a sonometer wire divided by a movable knife edge , differ in length by 2 mm and produce 1 beat//s , when sounded together . Find their frequencies if the whole length of wire is 1.00 m .
View SolutionTwo parts of sonometer wire, divided by a movable knife edge differ in length by 2 cm and produce 1 beat/s when sounded together. Assume fundamental frequencies. If the total length of the wire is 100 cm. The frequencies. If the total length of the wire is 100 cm. The frequencies of the two parts of the wire are
View SolutionTwo tuning forks when sounded together produce 4 beats per second. The first produces 8 beats per second. Calculate the frequency of the other.
View SolutionTwo notes A and B sounded together produce 2 beats per second. When notes B and C are sounded together 3 beats with per second are produced. The notes A and C separately produce the same number of beats with a standard tuning fork of frequency 456 Hz. The possible frequency of note B is
View SolutionProve the law of conservation of energy for a particle performing simple harmonic motion. Hence graphically show the variation of kinetic energy and potential energy w.r.t. instantaneous displacement.
Two sound notes have wavelengths 83170mand83172m in the air. These notes when sounded together produce 8 beats per second. Calculate the velocity of sound in the air and frequencies of the two notes.
View SolutionA knife edge divides a sonometer wire in two parts which differ in length by 2mm. The length of the wire is 1m. The two parts of the string when sounded together produce on beat per second, then the frequency of the smaller and the longer parts of the wire in Hz will be
View SolutionThe string of a violin emits a note of 205 Hz when its tension is correct. The string is made slightly more taut and it produces 6 beats in 2 seconds with a tuning fork of frequency 205 Hz. The frequency of the note emitted by the taut string is
View SolutionThe lengths of two taut strings are 70 cm and 60 cm respectively . If each of the two strings is sounded with a tuning fork, 5 beats are produced per second. What is the frequency of the tuning fork ?
View SolutionThe string of a sonometer is divided into two parts using wedge. Total length of string is 1m and two parts differ by 2mm . When sounded together they produce 2 beats/sec. The frequencies of two parts are
View SolutionA sonometer wire of 1 m length is divided into two parts by a movable bridge. The two parts differ by 3mm and produce two beats per second when sounded together. Find their frequencies.
View SolutionThe string of a sonometer is divided into two parts with the help of a wedge. The total length of the string is 1 m and the two parts differ by 2mm. When sounded together they produced two beats per second. The frequencies of the notes emitted by the two parts are
View Solution
