Time (T), velocity (C) and angular momentum (h) are chosen as fundamental quantities instead of mass, length and time. In terms of these, the dimensions of mass would be:
[M]−[T1C2h]
[M]=[T1Ch−1]
[M]=[T−1C−2h]
[M]=[TC−2h]
The correct Answer is:C
To find the dimensions of mass in terms of time (T), velocity (C), and angular momentum (h), we will follow these steps:
1. Understand the Dimensions of Fundamental Quantities:
- Time (T) has the dimension: (T)=T1
- Velocity (C) has the dimension: (C)=(L)(T)−1=L1T−1
- Angular momentum (h) has the dimension: (h)=(M)(L)2(T)−1=M1L2T−1
2. Set Up the Equation:
We want to express mass (M) in terms of T, C, and h. We can write:
M1=Tx⋅Cy⋅hz
Substituting the dimensions of C and h:
M1=Tx⋅(L1T−1)y⋅(M1L2T−1)z
3. Expand the Right Side:
Expanding the right side gives:
M1=Tx⋅LyT−y⋅MzL2zT−z
Combining the terms:
M1=Mz⋅Ly+2z⋅Tx−y−z
4. Equate the Powers:
Now, we equate the powers of M, L, and T from both sides:
- For M: 1=z
- For L: 0=y+2z
- For T: 0=x−y−z
5. Solve the Equations:
From 1=z, we have:
z=1
Substituting z=1 into 0=y+2z:
0=y+2⋅1⟹y=−2
Now substituting y=−2 and z=1 into 0=x−y−z:
0=x−(−2)−1⟹x+2−1=0⟹x=−1
6. Final Expression:
Now we have:
- x=−1
- y=−2
- z=1
Therefore, we can express mass (M) as:
M1=T−1⋅C−2⋅h1
Thus, the dimensions of mass in terms of T, C, and h are:
(M)=T−1C−2h1
Final Answer:
The dimensions of mass in terms of time (T), velocity (C), and angular momentum (h) are:
(M)=T−1C−2h1
- Time (T) has the dimension: (T)=T1
- Velocity (C) has the dimension: (C)=(L)(T)−1=L1T−1
- Angular momentum (h) has the dimension: (h)=(M)(L)2(T)−1=M1L2T−1
We want to express mass (M) in terms of T, C, and h. We can write:
M1=Tx⋅Cy⋅hz
Substituting the dimensions of C and h:
M1=Tx⋅(L1T−1)y⋅(M1L2T−1)z
Expanding the right side gives:
M1=Tx⋅LyT−y⋅MzL2zT−z
Combining the terms:
M1=Mz⋅Ly+2z⋅Tx−y−z
Now, we equate the powers of M, L, and T from both sides:
- For M: 1=z
- For L: 0=y+2z
- For T: 0=x−y−z
From 1=z, we have:
z=1
Substituting z=1 into 0=y+2z:
0=y+2⋅1⟹y=−2
Now substituting y=−2 and z=1 into 0=x−y−z:
0=x−(−2)−1⟹x+2−1=0⟹x=−1
Now we have:
- x=−1
- y=−2
- z=1
M1=T−1⋅C−2⋅h1
Thus, the dimensions of mass in terms of T, C, and h are:
(M)=T−1C−2h1
The dimensions of mass in terms of time (T), velocity (C), and angular momentum (h) are:
(M)=T−1C−2h1
Topper's Solved these Questions
- APPENDICES (REVISION EXERCISE)Book:AAKASH SERIESChapter:APPENDICES (REVISION EXERCISE)Exercise:MOTION IN A STRAIGHT LINE
Explore 59 Videos
- APPENDICES (REVISION EXERCISE)Book:AAKASH SERIESChapter:APPENDICES (REVISION EXERCISE)Exercise:MOTION IN A PLANE
Explore 87 Videos
- APPENDICES ( REVISION EXERCISE )Book:AAKASH SERIESChapter:APPENDICES ( REVISION EXERCISE )Exercise:REVISION EXERCISE (MAGNETISM AND MATTER )
Explore 52 Videos
- ATOMSBook:AAKASH SERIESChapter:ATOMSExercise:PRACTICE EXERCISE
Explore 21 Videos
Similar Questions
A particle transversed half of the distance with a velocity of V0. The remaining parts of the distance was covered with velocity Vl, for half of the time and with V2 for other half of the time. Find the mean velocity of the particle averaged and the whole time of motion.
View SolutionTwo vectors of equal magnitude P are inclined at some angle such that the difference in magnitude of resultant and magnitude of either of the vectors is 0.732 times either of the magnitude of vectors. If the angle between them is increased by half of its initial value then find the magnitude of difference of the vectors
View SolutionFind the resultant magnetic moment for the following arrangement
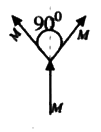
View SolutionThe energy of the electron in the ground state of hydrogen atom is −13.6eV. Find the kinetic energy of electron in this state.
View SolutionIf the velocity (V) , acceleration (A) , and force (F) are taken as fundamental quantities instead of mass (M) , length (L),andtime(T) , the dimensions of young's modulus (Y) would be
View SolutionIf units of length, mass and force are chosen as fundamental units, the dimensions of time would be :
View SolutionTime (T), velocity (3) and angular momentum (h) are chosen as fundamental quantities instead of mass, length and time. In terms of these, the dimensions of mass would be
View SolutionIf the velocity of light c, Plank s constant, h and the gravitational constant G are taken as fundamental quantities, then express mass, length and time in terms of dimensions of these quantities.
View SolutionIf the velocity (V), acceleration (A) and force (F) are taken as fundamental quantities instead of mass (M), length (L) and time (T), the dimensions of young's modulus (Y) would be :
View SolutionIf units of length, mass and force are chosen as fundamental units, the dimensions of time would be :
View SolutionTime (T), velocity (C) and angular momentum (h) are chosen as fundamental quantities instead of mass, length and time. In terms of these, the dimensions of mass would be:
View SolutionIf velocity of light c, Planck's constant h and gravitational constant G are taken as fundamental quantities, then express mass, length and time in terms of dimensions of these quantities.
View SolutionTime (T), velocity (C) and angular momentum (h) are chosen as fundamental quantities instead of mass, length and time. In terms of these, the dimensions of mass would be
View SolutionTime (T), velocity (C) and angular momentum (h) are chosen as fundamental quantities instead of mass, length and time. In terms of these, the dimensions of mass would be
View SolutionTime (T), velocity (C) and angular momentum (h) are chosen as fundamental quantities instead of mass, length and time. In terms of these, the dimensions of mass would be:
View SolutionTime (T), velocity (C) and angular momentum (h) are chosen as fundamental quantities instead of mass, length and time. In terms of these, the dimensions of mass would be:
View Solution
