An impulse →I changes the velocity of a particle from →v1 to →v2. Kinetic energy gained by the particle is :-
I(v1+v2)
I(v1+v2)/2
I(v1−v2)
I(v1−v2)/2
The correct Answer is:B
Step by step video solution for An impulse vec(I) changes the velocity of a particle from vec(v)_(1) to vec(v)_(2). Kinetic energy gained by the particle is :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - I
157 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
7 Videos
Similar Questions
A force of 50 N acts on a body of mass 10 kg at rest. Its velocity after 5 seconds if the same force acts, is
View SolutionTo keep a particle moving with constant velocity on a frictionless horizontal surface an external force
View SolutionA light beam is traveling from Region I to region IV (refer figure). The refractive indices in Region I, II, III, and IV are n0,n0/2,n0/6andn0/8 , respectively. The angle of incidence θ for which the beam just misses entering Region IV is
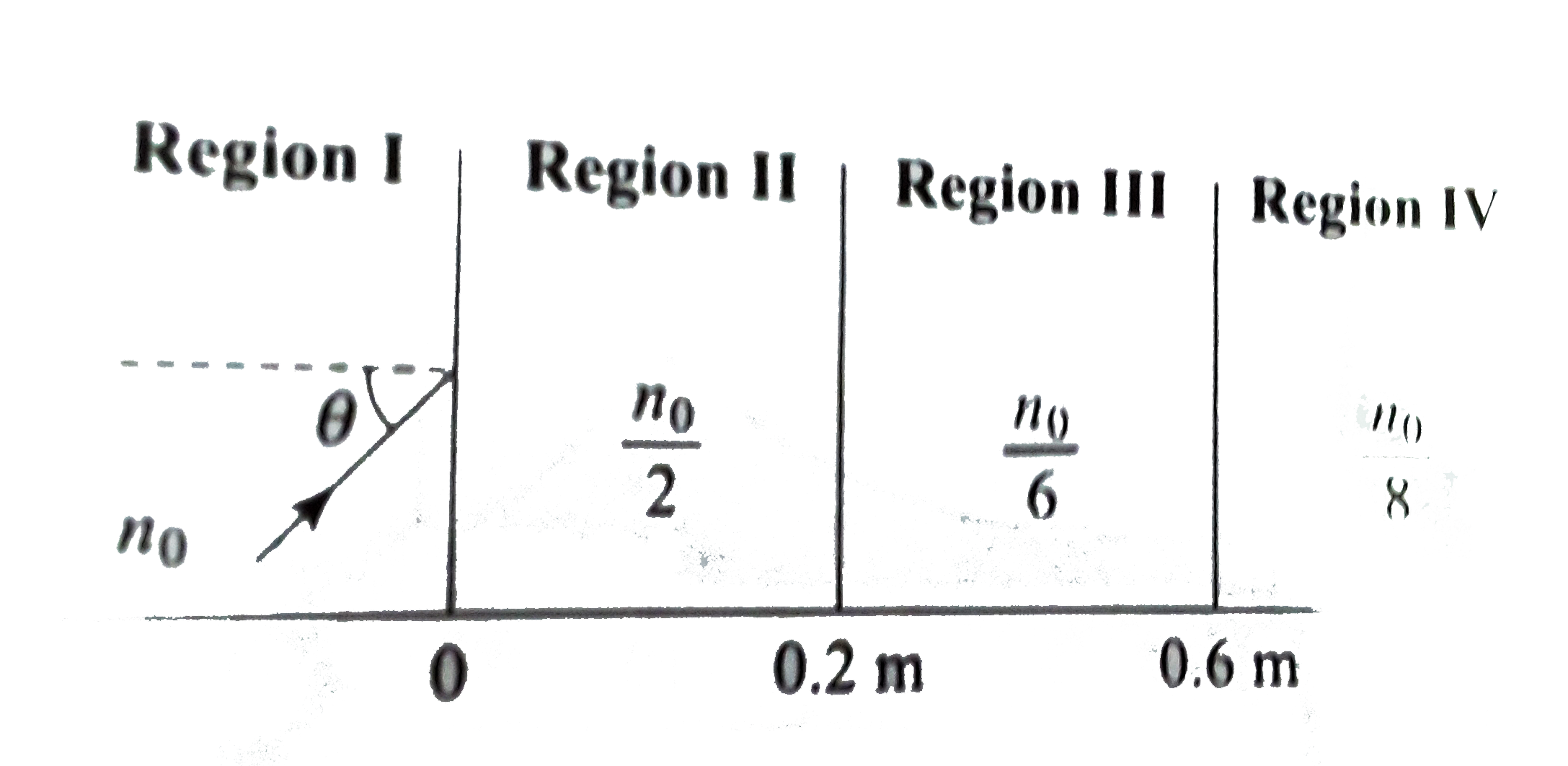
View Solution
The output C in the above circuit is given by C = ---
View SolutionIf →v1+→v2 is perpendicular to →v1−→v2, then
View SolutionTwo particles of masses m_(1) and m_(2) in projectile motion have velocities vec(v)_(1) and vec(v)_(2) , respectively , at time t = 0 . They collide at time t_(0) . Their velocities become vec(v')_(1) and vec(v')_(2) at time 2 t_(0) while still moving in air. The value of |(m_(1) vec(v')_(1) + m_(2) vec(v')_(2)) - (m_(1) vec(v)_(1) + m_(2) vec(v)_(2))|
View SolutionAn impulse vrc(I) changes the velocity of a particle from →v1 to vrc(v)2. Kinetic energy gained by the particle is :-
View SolutionA moving particle of mass m collides elastically with a stationary particle of mass 2m. After collision the two particles move with velocity →v1 and →v2 respectively. Prove that →v2 is perpendicular to (2→v1+→v2)
View SolutionThe velocity of a particle varies with time as per the law →v=→a+→b t where →a and →b are two constant vectors. The time at which velocity of the particle at t=0 is :
View SolutionIf two bodies are in motion with velocity →v1 and →v2:
View SolutionIf ∣∣→V1+→V2∣∣=∣∣→V1−→V2∣∣andV2 is finite, then
View SolutionA nucleus moving with a velocity vec(v) emits an alpha - particle. Let the velocities of the alpha - particle and the remaining nucleus be vec(v)_(1) and vec(v)_(2) and their masses be m_(1) and m_(2) .
View SolutionThe velocity of a particle varies with time as per the law vec(V) = vec(a) + vec(b)t where vec(a) and vec(b) are two constant vectors. The time at which velocity of the particle is perpendicular to velocity of the particle at t= 0 is
View SolutionA nucleus moving with a velocity →v emits an α - particle. Let the velocities of the α - particle and the remaining nucleus be →v1 and →v2 and their masses be m1 and m2.
View SolutionIf ∣∣→V1+→V2∣∣=∣∣→V1−→V2∣∣andV2 is finite, then
View SolutionIf →v1+→v2 is perpendicular to →v1−→v2, then
View Solution

