Acceleration of block parallel to plane (if M=2m,θ=45,μ=0.5)
5g9√2
5g18√2
5g3√2
5g8√2
The correct Answer is:A
To solve the problem of finding the acceleration of a block on an inclined plane, we can follow these steps:
Step 1: Understand the Problem
We have a block of mass M=2m on an inclined plane with an angle θ=45∘ and a coefficient of friction μ=0.5. We need to find the acceleration of the block parallel to the plane.
Step 2: Draw the Free Body Diagram
1. Draw the inclined plane and the block on it.
2. Identify the forces acting on the block:
- Weight acting downwards: W=2mg
- Normal force N acting perpendicular to the inclined plane
- Frictional force f acting parallel to the plane (upwards, opposing motion)
Step 3: Resolve Forces
1. Resolve the weight into components:
- Parallel to the plane: W∥=2mgsin(45∘)=2mg⋅1√2=2mg√2
- Perpendicular to the plane: W_{\perpendicular} = 2mg \cos(45^\circ) = 2mg \cdot \frac{1}{\sqrt{2}} = \frac{2mg}{\sqrt{2}}
Step 4: Calculate Normal Force
The normal force N is equal to the perpendicular component of the weight:
N = W_{\perpendicular} = \frac{2mg}{\sqrt{2}}
Step 5: Calculate Maximum Static Friction
The maximum static friction fs can be calculated using:
fs=μN=μ(2mg√2)=0.5⋅2mg√2=mg√2
Step 6: Calculate Net Force
The net force Fnet acting on the block parallel to the incline is given by:
Fnet=W∥−fs
Substituting the values:
Fnet=2mg√2−mg√2=mg√2
Step 7: Calculate Acceleration
Using Newton's second law, F=ma:
a=Fnetmass=mg√22m
This simplifies to:
a=g2√2
Final Answer
The acceleration of the block parallel to the plane is:
a=g2√2
---
We have a block of mass M=2m on an inclined plane with an angle θ=45∘ and a coefficient of friction μ=0.5. We need to find the acceleration of the block parallel to the plane.
1. Draw the inclined plane and the block on it.
2. Identify the forces acting on the block:
- Weight acting downwards: W=2mg
- Normal force N acting perpendicular to the inclined plane
- Frictional force f acting parallel to the plane (upwards, opposing motion)
1. Resolve the weight into components:
- Parallel to the plane: W∥=2mgsin(45∘)=2mg⋅1√2=2mg√2
- Perpendicular to the plane: W_{\perpendicular} = 2mg \cos(45^\circ) = 2mg \cdot \frac{1}{\sqrt{2}} = \frac{2mg}{\sqrt{2}}
The normal force N is equal to the perpendicular component of the weight:
N = W_{\perpendicular} = \frac{2mg}{\sqrt{2}}
The maximum static friction fs can be calculated using:
fs=μN=μ(2mg√2)=0.5⋅2mg√2=mg√2
The net force Fnet acting on the block parallel to the incline is given by:
Fnet=W∥−fs
Substituting the values:
Fnet=2mg√2−mg√2=mg√2
Using Newton's second law, F=ma:
a=Fnetmass=mg√22m
This simplifies to:
a=g2√2
The acceleration of the block parallel to the plane is:
a=g2√2
Similar Questions
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionAcceleration of block m is (θ<45∘)
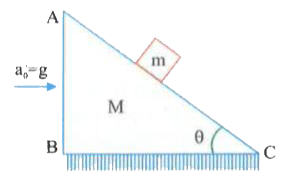
View SolutionA block of mass 2kg is lying on a rough inclined plane. The force needed to move the block up the plane with uniform velocity by applying a force parallel to the plane is 100N. The force needed to move the block up with an accele-ration of 2ms−2 is
View SolutionAcceleration of block 'm' is (θ<45∘)
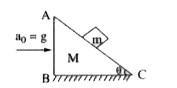
View SolutionA block of mass m and a cylinder of mass 2m are released on a rough inclined plane, inclined at angle theta=45^(@) with the horizontal. The coefficient of friction for all the contact surface is 0.5 Find the accelerations of the block and the cylinder. Assume pure rolling 3g//xsqrt(2) where 'x' is
View SolutionA block of mass m is kept over another block of mass 2m. Coefficient of friction between two blocks is μ and that of between lower blood from the horizontal surface is zero. A horizontal force F=43μmg is applied on the block of mass 2m. Acceleration of lower block is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination theta . If coefficient of friction between the block and the inclined plane is mu , then the minimum value of force along the plane required to move the block on the plane is
View Solution

