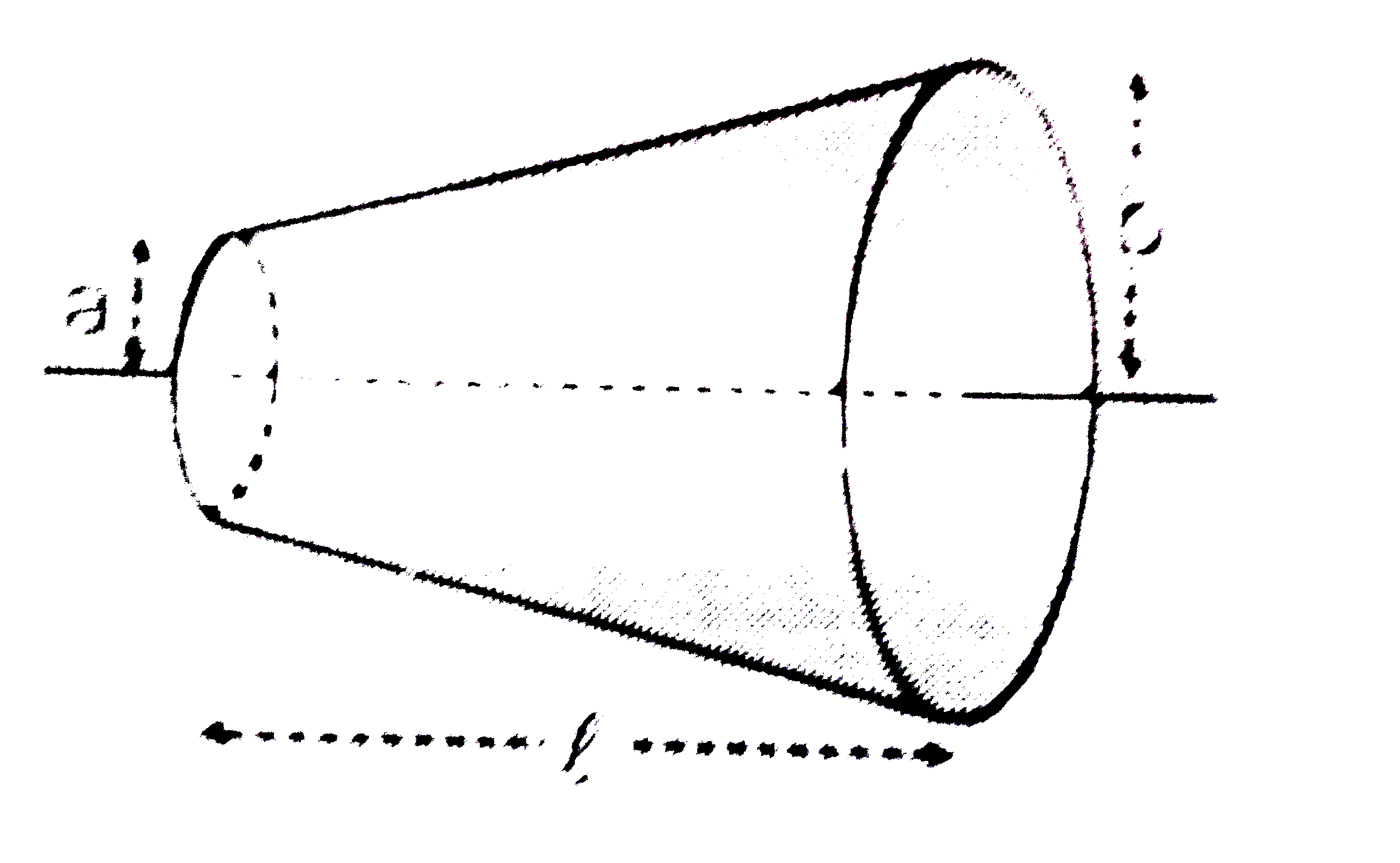
Figure shows a conductor of length l carrying current i and having a circular cross-section. The radius of cross section varies linearly from a to b. assuming that (b−a)<<l calculate current density at distance x from left end.
 Solution in Gujrati
Solution in Gujrati
dRdue→thesmallstripdxatadistance<br>y,R = (rhodx/ y_2)…….(i)<br> tan theta = ((y-a)/x) = ((b-a)/L)<br> rArr ((y-a)/x) = ((b-a)/L)<br> rArr L xx ( y-a) = x(b-a)<br> rArr Ly - La = xb - xa <br> rArr L dy/dx -0 = b-a (diff. w.r. t. x) <br> dx = Ldy/ (b-a)<br>Pu∈gthevalueofdx∈eqn.(i)
dR=(ρLdyπ(y2)(b−a))
dR=(ρLπ(b−a)).dyy2
⇒(∫R0)dR=(ρLπ(b−a))(∫ba)dyy2
R=(ρLπ(b−a))([−1y]ba)
=(ρLπ(b−a))(−1b)(−1a)
(ρLπab).
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBook:HC VERMAChapter:ELECTRIC CURRENT IN CONDUCTORSExercise:Objective 2
Explore 9 Videos
- DISPERSION AND SPECTRABook:HC VERMAChapter:DISPERSION AND SPECTRAExercise:Exercises
Explore 11 Videos
- ELECTRIC CURRENT THROUGH GASESBook:HC VERMAChapter:ELECTRIC CURRENT THROUGH GASESExercise:Exercises
Explore 23 Videos
Similar Questions
Electrons are emitted by a hot filament and are accelerated by an electric field as shown in figure .The two stops at the left ensure that the electron beam has a uniform cross-section.

View SolutionA flint glass prism and a crown glass prism are to be combined in such a way that the deviation of the mean ray is zero. The refractive index of flint and crown glasses for the mean ray are 1.620 and 1.518 respectively. If the refracting angle of the flint prism is 6.0∘, what would be the refracting angle of the crown prism ?
View SolutionA discharge tube contains helium at a low pressure. A large potential difference is applied across the tube. Consider a helium atom that has just been ionized due to the detachment of an atomic electron. Find the ratio of the distance travelled by the free electron to that by the positive ion in a short time dt after the ionization.
View SolutionShown a conductor of length l having a circular cross section. The radius of cross section varies linearly form a→b. The resistivity of the material is(ρ).Assuming that b−a<<l,find the resistance of the conductor.

View SolutionA conductor of length l has a non-uniform cross-section. The radius of cross-section varies linearly from a to b. The resistivity of the material is ρ. Find the resistance of the conductc across its ends.

View SolutionIn a long wire of square cross-section of side length l, current density varies with distance x from one edge of cross-section as
J=aehxA/m2
Where a and b are positive constants. Find the current flowing in wire.
[alb(e−1)]
View SolutionThe figure shows a long striaght wire of a circular cross-section (radius a) carrying steady current I.The current I is unifromly distributed across this distance a/2 and 2a from axis is
View SolutionFigure shows a conductor of length l having a circular cross-section. The radius of cross-section varies linearly from a to b. Find the resistance of the conductor. ltbtgt
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionFigure shows a conductor of length l having a circular cross section. The radius of cross section of the conductor varies linearly from r1 to r2 along its length. IF the specific resistance of the material of the conductor be ρ, find the resistance of the conductor.
View SolutionThe figure shows the cross-section of a long cylindrical conductor of radius a carrying a uniformly distributed current i. The magnetic field due to current at P is :
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.
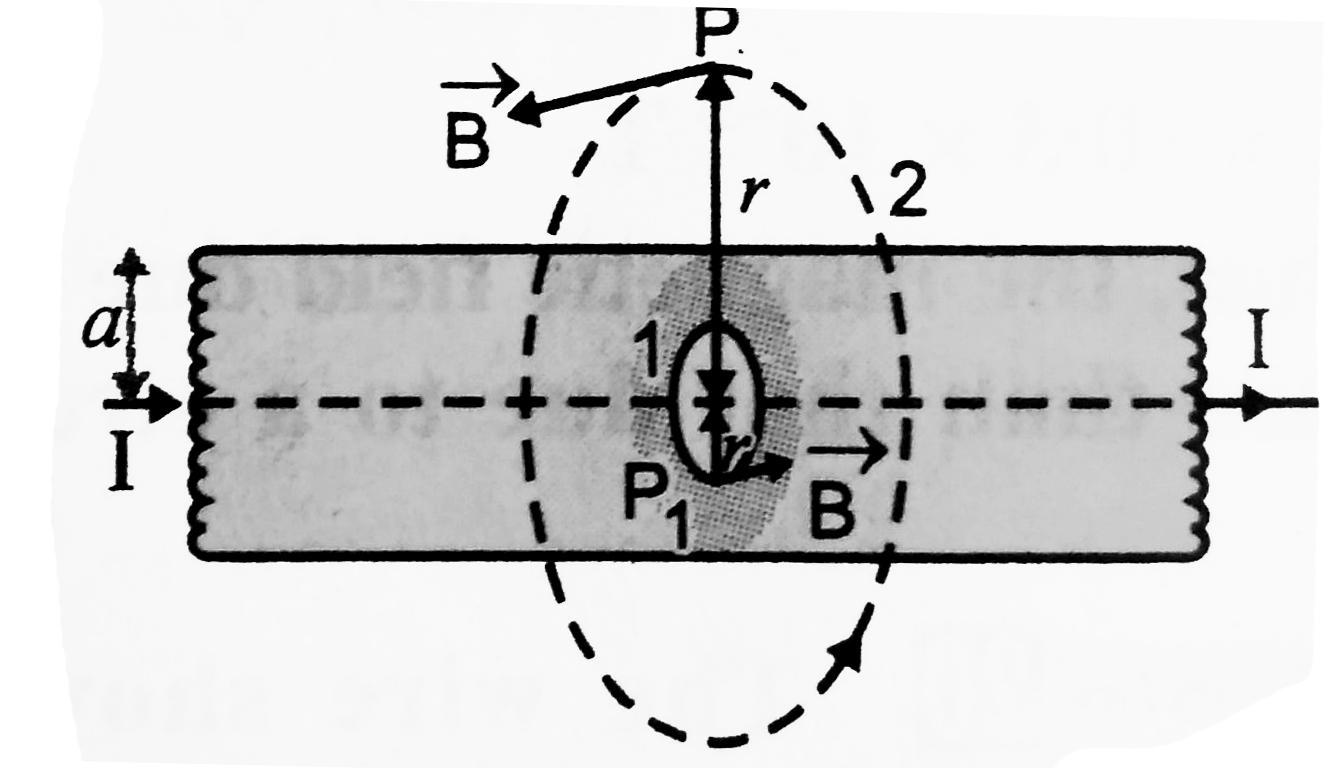
View SolutionFigure shows a long straight wire of a circular cross - section (radius a) carrying steady current I. The current I is uniformly distributed across this cross - section . Calculate the magnetic field in the region r lt a and r gt a
View SolutionThe adjoining figure shows a long straight wire of a circular cross section (radius a) carrying steady current I. The current I is uniformly distributed across its cross section. Calculate the magnetic field at a distance from its axis for (i) r lt a , (ii) r gt a .
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current I. The current I is uniformly distributed across this cross-section. Calculate the magnetic field in the region r a.
View SolutionShown a conductor of length l having a circular cross section. The radius of cross section varies linearly form a→b. The resistivity of the material is(ρ).Assuming that b−a<<l,find the resistance of the conductor.

View Solution
