A block of mass m is kept on a smooth surface. It is also in contact with a thin plank of mass M=2m, one end of which is clamped to a wall as shown in the figure. The length of the plank is L. The block is given an initial velocity v0, towards right and initially the block is at a distance x0 from hinge. Coefficient of friction between the plank and block is μ.
Assume that througout the motion block remains, below the rod, then at what position from the fixed point it will stop?
(GIven β=v202μgL)
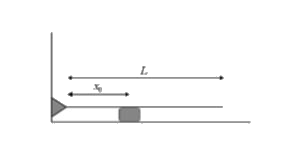
x0e2β
x0eβ
x0e−2β
x0e−β
The correct Answer is:B
a=−μgL2xm=vdvdx
Topper's Solved these Questions
Similar Questions
The rate of disintegration of a radioactive sample can be increased by :-
View SolutionA redioctive nucleus decays as follows :
Xα−−→X1β−−→X2α−−→X3α−−→X4
If the atomic number and the mass number of X are 72 and 180 then the mass number and atomic number of X4 are-
View SolutionFigure shown a small block A of mass m kept at the left end of a plank B of mass M = 2m and length l . The system can side on a horizontal rood. The system is started towards right with the initial velocity v . The friction coefficient between the rood and the plank is 1//2 and that between the plank and the block is 1//4 . Find (a) the time elapsed before the block separates from the plank (b) displacement of block and plank relative to ground till that moment.
View SolutionA small block of mass m is plced over a long plank of mass M the coefficient of friction between then is μ ground is smooth At t=0 m is given a velocity v1 and M a velocity v2(>v1) as shown in figure After this M is maintained at constant celeration a(<μg)
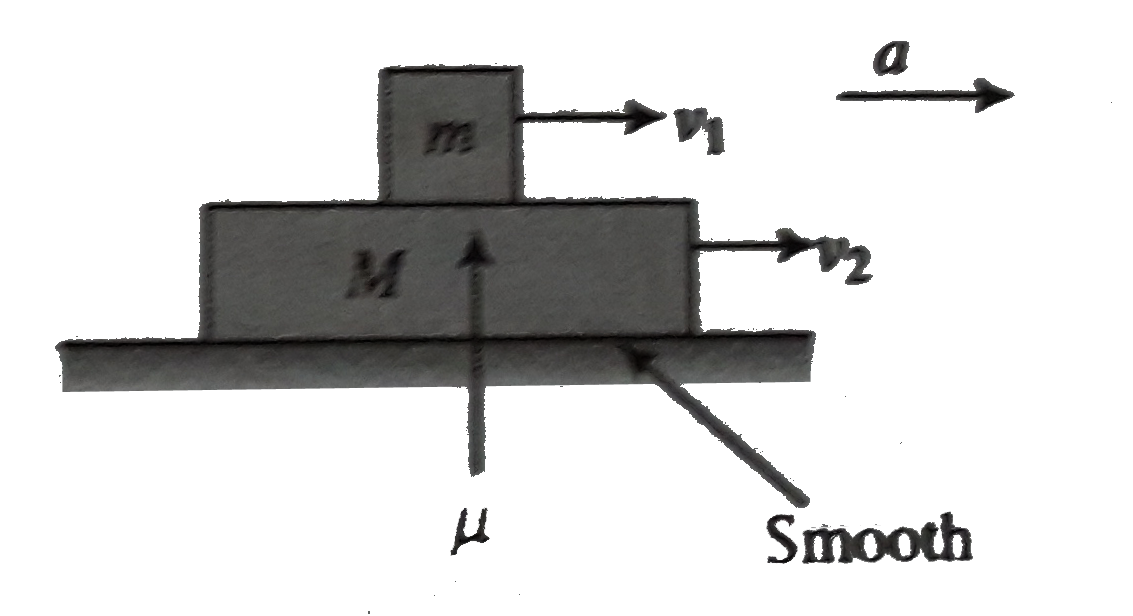
Initially there will be some relative motion between the block and the plank ,but after some time relative motion will cease and velocities of both will become
Find the forward force acting on the plank before after t0 respectively.
View SolutionA block A of mass m is placed over a plank B of mass 2m plank B is placed over a smooth horizontal surface .The coefficient of friction between A and B is 0.4 Block A is given a velocity v_(0) toward right Find acceleration (in ms^(-2) of B relative to A
View SolutionA block of mass m is pushed with a velocity v0 along the surface of a trolley car of mass M. If the horizontal ground is smooth and the coefficient of kinetic friction between the block of plank is μ. Find the minimum distance of relative sliding between the block and plank.

View SolutionA block A of mass m is over a plank B of mass 2m . Plank B si placed over a smooth horizontal surface. The coefficient of friction between A and B is (1)/(2) . Blocks A is given a velocity V_(0) towards right. Then
View SolutionA plank of length 20m and mass 1kg is kept on a horizontal smooth surface. A cylinder of mass 1lg is kept near one end of the plank. The coefficient of friction between the two surface is 0.5. The plank is suddenly given a velocity 20m/s towards left

Which of the following statements is correct?
View SolutionThe block of mass m is kept on plank of mass M. The block is given velocity V_(0) as shown. The coefficient of friction between the block of mass m and plank of mass M is mu and its value is such that block becomes stationary with respect to plank before it reaches the other end. Then:
View SolutionA block A of mass m is placed over a plank B of mass 2m. Plank B is placed over a smooth horizontal surface. The coefficient of friction between A and B is 12 block A is given a velocity v0 towards right. Accelration of B relative to A is

View SolutionIn the arrangement shown in figure , there is friction between the blocks of masses m and 2m which are in contact . The ground is smooth . The mass of the suspended block is m . The block of mass m which is kept on mass 2m is stationary with respect to block of mass 2 m . The force of friction between m and 2 m is (pulleys and string are lig frictionless ) :

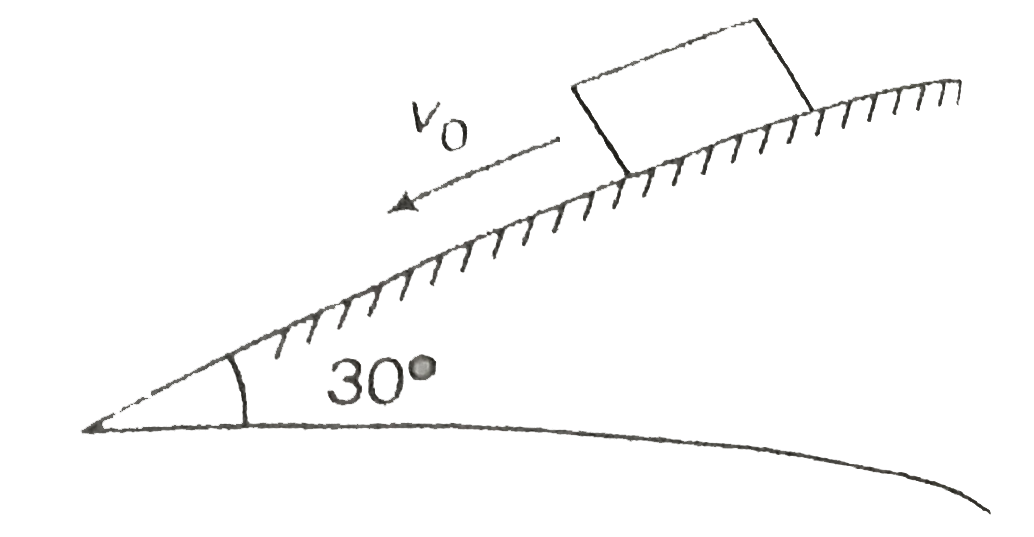
View SolutionA block of mass m is given an initial downward velocity v0 and left on inclined place ( coefficient of friction =0.6). The block will
View SolutionFigure shown a small block A of mass m kept at the left end of a plank B of mass M=2m and length l . The system can slide on a horizontal road. The system is started towards right with the initial velocity v. The friction coefficient between the road and the plank is 1/2 and that between the plank and the block is 1/4 . Find

(a) the time elapsed before the block separates from the plank
(b) displacement of block and plank relative to ground till that moment.
View SolutionA block A of mass m is placed over a plank B of mass 2m. Plank B is placed over a smooth horizontal surface. The coefficient of friction between A and B is 12 block A is given a velocity v0 towards right. Accelration of B relative to A is

View SolutionA block of mass m is given an initial downward velocity v_(0) and left on inclined place ( coefficient of friction =0.6). The block will
View SolutionThe block of mass m is kept on plank of mass M. The block is given velocity V_(0) as shown. The coefficient of friction between the block of mass m and plank of mass M is mu and its value is such that block becomes stationary with respect to plank before it reaches the other end. Then:
View Solution

