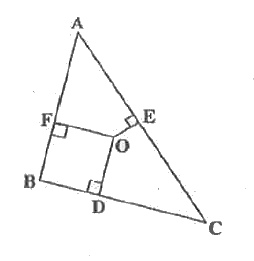
In fig., O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that:- OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
To solve the problem, we need to prove the equation:
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
where O is a point inside triangle ABC, and OD, OE, and OF are perpendiculars dropped from O to the sides BC, AC, and AB respectively.
1. Identify Right Triangles:
We have three right triangles formed by the perpendiculars:
- Triangle OAF (with right angle at F)
- Triangle OBD (with right angle at D)
- Triangle OEC (with right angle at E)
2. Apply Pythagorean Theorem:
For each of these triangles, we can apply the Pythagorean theorem.
- For triangle OAF:
OA2=AF2+OF2(1)
- For triangle OBD:
OB2=OD2+BD2(2)
- For triangle OEC:
OC2=OE2+CE2(3)
3. Rearranging the Equations:
We can rearrange these equations to express OF2, OD2, and OE2 in terms of the other sides:
- From equation (1):
OF2=OA2−AF2(4)
- From equation (2):
OD2=OB2−BD2(5)
- From equation (3):
OE2=OC2−CE2(6)
4. Substituting Back:
Now we substitute equations (4), (5), and (6) back into the original equation we want to prove:
OA2+OB2+OC2−(OB2−BD2)−(OC2−CE2)−(OA2−AF2)=AF2+BD2+CE2
5. Simplifying the Left Side:
Simplifying the left side:
OA2+OB2+OC2−OB2+BD2−OC2+CE2−OA2+AF2
This simplifies to:
AF2+BD2+CE2
6. Conclusion:
Thus, we have shown that:
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
Hence, the statement is proved.
We have three right triangles formed by the perpendiculars:
- Triangle OAF (with right angle at F)
- Triangle OBD (with right angle at D)
- Triangle OEC (with right angle at E)
For each of these triangles, we can apply the Pythagorean theorem.
OA2=AF2+OF2(1)
- For triangle OBD:
OB2=OD2+BD2(2)
- For triangle OEC:
OC2=OE2+CE2(3)
We can rearrange these equations to express OF2, OD2, and OE2 in terms of the other sides:
- From equation (1):
OF2=OA2−AF2(4)
- From equation (2):
OD2=OB2−BD2(5)
- From equation (3):
OE2=OC2−CE2(6)
Now we substitute equations (4), (5), and (6) back into the original equation we want to prove:
OA2+OB2+OC2−(OB2−BD2)−(OC2−CE2)−(OA2−AF2)=AF2+BD2+CE2
Simplifying the left side:
OA2+OB2+OC2−OB2+BD2−OC2+CE2−OA2+AF2
This simplifies to:
AF2+BD2+CE2
Thus, we have shown that:
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
Hence, the statement is proved.
Topper's Solved these Questions
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - NCERT CORNER ( TEXTBOOK QUESTIONS) ( EXERCISE - 6.6 )
12 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - NCERT EXEMPLAR ( EXERCISE - 6.1 )
12 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - NCERT CORNER ( TEXTBOOK QUESTIONS) ( EXERCISE - 6.4 )
9 Videos
- SURFACE AREAS AND VOLUMES BOOK - OSWAL PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
9 Videos
Similar Questions
In the figure given below PS is the bisector of ∠QPR of ΔPQR . Prove that QSSR=PQPR .

View SolutionIn the figure given below ∠BAC=90∘ and AD ⊥ BC. Then
View SolutionLet ΔABC~ΔDEF and their areas be respectively 64 cm2 and 121cm2 . If EF = 15.4 cm find BC .
View SolutionA bucket is in form of a frustum of a cone with a copacity of 12308.8cm3of water. The radii of the tope bottom circular ends are 20 cm and 12 cm respectively. Find the height of the bucket and the area of the metal sheet used in its making. [ Use π=3.14.]
View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2

View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
View SolutionIf O and O′ are circumcentre and orthocentre of ABC, then →OA+→OB+→OC equals
a.2→OO' b. →OO' c. →O'O d. 2→O'O
View SolutionIn Fig. 2.54, o is a point in the interior of a triangle ABC,OD⊥BC,OE⊥ACandof⊥AB. Show that
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2,
View SolutionO is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2

View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View SolutionO is any point inside a triangle ABC . The bisector of ∠AOB,∠BOC and ∠COA meet the sides AB,BC and CA in point D,EandF respectively. Show that AD⋅BE⋅CF=DB⋅EC⋅FA
View SolutionFrom a point O in the interior of a ABC , perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: (i) AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2 (ii) AF2+BD2+CE2=AE2+CD2+BF2
View SolutionA point O in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D . Prove that OB2+OD2=OC2+OA2
View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View Solution
