Find the value of'
Video Solution
Text Solution
(i) Let y−(x2−3x2+4)(4x5_x2−1)
dydx=(x303x2+4)ddx(4x5)+ddx(x2)−ddx(1)+(4x5+x2−1)[ddx(x3)−ddx(3x2)+ddx(4)]
(x3−3x2+4)[4ddx(x5)+ddx(x2)−ddx(1)]+(4x5+x2−1)[ddx(x3)−3ddx(x2)+ddx(4)]
=(x3−3x2+4)(20x4+2x)+(4x5_x2−1)(3x2−6x) ltbr> =2x(10x3+1)(x2−3x2+4)+3x(x−2)(4x3+x2−1)
(ii) Let y=9x5x−3
dydx=(x−3)ddx(9x5)−9x5ddx(x−3)(x−3)2
=(x−3)×9ddx(x5)−9x5[ddx(x)−ddx(3)](x−3)2=(x−3)×9×5x4−9x5(1−0)(x−3)2
=45x50135x4−9X5(x−3)2=36x5−135x4(x−3)2=9x4(4x015)(x−3)2
|
Similar Questions
Find the values of (12)−5
View SolutionFind the values of
(i)(12)−1<br>(ii)13−4
View SolutionFind the values of 3−1+4−1
View SolutionFind the values of (12)−1+(13)−1+(14)−1
View SolutionFind the values of sin75∘.
View SolutionFind the values of A,B and C
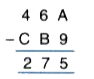
View SolutionFind the values of x and y.
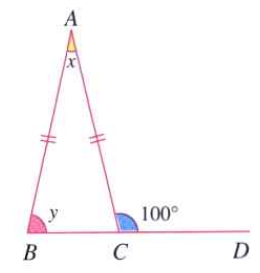
View SolutionFind the values of
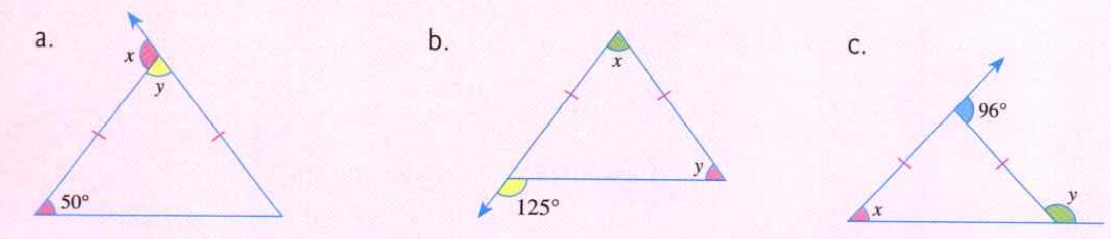
x and y.
View SolutionFind the values of A and B.
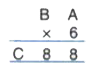
View SolutionFind the values of cosπ8
View Solution
