A car travels a distance of 840 km at a uniform speed if speed is 10 km/hr more it take two hour less original speed of car is
A)45 km/hr
B)50km/hr
C)60km/hr
D)75 km/hr
The correct Answer is:C
To solve the problem, we will use the relationship between distance, speed, and time. The formula we will use is:
Distance=Speed×Time
1. Define Variables:
Let the original speed of the car be x km/hr.
2. Calculate Time at Original Speed:
The time taken to travel 840 km at the original speed x is given by:
Time=DistanceSpeed=840x
3. Calculate Time at Increased Speed:
If the speed is increased by 10 km/hr, the new speed becomes x+10 km/hr. The time taken to travel the same distance at this new speed is:
Time=840x+10
4. Set Up the Equation:
According to the problem, the time taken at the increased speed is 2 hours less than the time taken at the original speed. Therefore, we can set up the equation:
840x−840x+10=2
5. Solve the Equation:
To solve the equation, first find a common denominator:
840(x+10)−840xx(x+10)=2
Simplifying the numerator:
840x+8400−840xx(x+10)=2
This simplifies to:
8400x(x+10)=2
6. Cross-Multiply:
Cross-multiplying gives:
8400=2x(x+10)
7. Expand and Rearrange:
Expanding the right side:
8400=2x2+20x
Rearranging gives:
2x2+20x−8400=0
8. Divide by 2:
To simplify, divide the entire equation by 2:
x2+10x−4200=0
9. Use the Quadratic Formula:
We can solve this quadratic equation using the quadratic formula:
x=−b±√b2−4ac2a
Here, a=1,b=10,c=−4200:
x=−10±√102−4⋅1⋅(−4200)2⋅1
x=−10±√100+168002
x=−10±√169002
x=−10±1302
10. Calculate Possible Values:
This gives us two possible solutions:
x=1202=60(valid speed)
x=−1402=−70(not valid)
11. Conclusion:
The original speed of the car is 60 km/hr.
Let the original speed of the car be x km/hr.
The time taken to travel 840 km at the original speed x is given by:
Time=DistanceSpeed=840x
If the speed is increased by 10 km/hr, the new speed becomes x+10 km/hr. The time taken to travel the same distance at this new speed is:
Time=840x+10
According to the problem, the time taken at the increased speed is 2 hours less than the time taken at the original speed. Therefore, we can set up the equation:
840x−840x+10=2
To solve the equation, first find a common denominator:
840(x+10)−840xx(x+10)=2
Simplifying the numerator:
840x+8400−840xx(x+10)=2
This simplifies to:
8400x(x+10)=2
Cross-multiplying gives:
8400=2x(x+10)
Expanding the right side:
8400=2x2+20x
Rearranging gives:
2x2+20x−8400=0
To simplify, divide the entire equation by 2:
x2+10x−4200=0
We can solve this quadratic equation using the quadratic formula:
x=−b±√b2−4ac2a
Here, a=1,b=10,c=−4200:
x=−10±√102−4⋅1⋅(−4200)2⋅1
x=−10±√100+168002
x=−10±√169002
x=−10±1302
This gives us two possible solutions:
x=1202=60(valid speed)
x=−1402=−70(not valid)
The original speed of the car is 60 km/hr.
টপার এই প্রশ্নগুলো সমাধান করেছে
সম্পর্কিত প্রশ্ন
Following table gives the population of a from 1998 to 1992
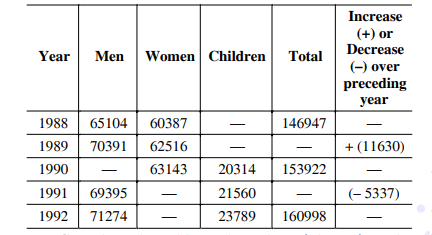
Complete the table and mark a tick against the correct answer in the question ------
View SolutionDinesh and Ram can do a working 80 minutes and 120 minutes respectively. In how much time this work will be completed if they work altogether ?
View SolutionA car takes 5 hours to reach a destination by travelling at the speed of 60 km/hr. How long will it take when the car travels at the speed of 75 km/hr?
View SolutionA car takes 2 hours to reach a destination by travelling at the speed of 60 km/hr.How long it take when the car travels at the speed of 80 km/hr?
View Solutionकिसी निश्चित चाल से एक कार P से Q की दुरी पर करती है यदि इसकी चाल 7 कि.मी./घर बढ़ा दी जाती है तो इसे दूरी तय करने में एक घण्टा कम लगता है। यदि इसकी चाल 5 कि.मी./घंटा कम जाती है तो इसे 1 घंटा ज्यादा लगते है। तो दोनो शहरो P तथा Q के बीच की दूरी तथा कार की चाल ज्ञात करो।
View SolutionA person travelled 270 km in 9 hours partly by car and partly by train. Speed of car is 36 km/h and speed by train is 27 km/hr. Find the distance travelled by car and travelled by train.
View SolutionA car with a uniform speed travels a distance of 165 km in 3 hours. At that same speed,
how long will it take to cover a distance of 330 km?
View SolutionA car with a uniform speed travels a distance of 165 km in 3 hours. At that same speed,
how far will it travel in 8 hours ?
View SolutionA car with a uniform speed travels a distance of 165 km in 3 hours. At that same speed,
how long will it take to cover a distance of 330 km?
View SolutionA car with a uniform speed travels a distance of 165 km in 3 hours. At that same speed,
how far will it travel in 8 hours ?
View SolutionA car covers 25 km at a uniform speed. If the speed had been 8 km/h more, it would have taken 10 hours less for the same journey. What is the speed of the car (in km/h)?
एक कार 25 किमी की दूरी एक समान चाल से तय करती है | यदि चाल 8 किमी/घंटा अधिक होती, तो इसे इस यात्रा में 10 घंटे कम लगते | कार की चाल ( किमी/घंटा में)कितनी है?
View SolutionIf the speed of a car was 10 km/h less, it would have traveled 840 km. It would have taken 2 hours more to cover the distance, find the actual speed of the car
View SolutionIf a car traveling at the same speed covers a distance of 240 km in 4 hours then (a) How much time will it take to travel 180 km at his speed? (b) What distance will the car cover in 5 hours with the same speed?
View SolutionA car covers a distace of 480 km at a uniform speed. If the speed of the car is 20 km/hour more, it takes 2 hours less to cover the same distance. What was the original speed of the car?
View SolutionA car covers a certain distance in 5 hours at the speed of 73 kms/hr. What is the average speed of bus which travels a distance of 50 kms less than the car in the same time ? Options are (a) 61 km/hr (b) 58 km/hr (c) 65 km/hr (d) 63 km/hr.
View SolutionA car travels a distance of 480 km at a uniform speed. Had the speed of the car been 20 km/h more, it would have taken 2 hours less to cover the same distance. What was the actual speed of the car?
View Solution
