If AD is a median of a ΔABC and P is a point on AC such that ar(ΔADP) : ar (ΔABD) = 2:3, then ar (ΔPDC) : ar (ΔABC) is .
1:6
1:5
2:5
3:5
The correct Answer is:A
To solve the problem, we will follow these steps:
1. Understand the Given Information: We have triangle ABC with AD as a median. This means D is the midpoint of BC. We also know that the area of triangle ADP is in the ratio of 2:3 with the area of triangle ABD.
2. Assign Variables: Let's denote the area of triangle ABD as X. Since D is the midpoint, the area of triangle ACD will also be X.
3. Calculate the Area of Triangle ADP: Given that the area of triangle ADP to the area of triangle ABD is 2:3, we can express the area of triangle ADP as:
Area of △ADP=23×X=2X3
4. Calculate the Area of Triangle ADC: The area of triangle ADC is equal to the area of triangle ABD, which we have already defined as X.
5. Find the Area of Triangle PDC: To find the area of triangle PDC, we can use the relationship:
Area of △ADC=Area of △ADP+Area of △PDC
Therefore, we can express the area of triangle PDC as:
Area of △PDC=Area of △ADC−Area of △ADP
Substituting the values we have:
Area of △PDC=X−2X3=3X3−2X3=X3
6. Calculate the Area of Triangle ABC: The area of triangle ABC is the sum of the areas of triangles ABD and ACD:
Area of △ABC=Area of △ABD+Area of △ACD=X+X=2X
7. Find the Ratio of Areas: Now we can find the ratio of the area of triangle PDC to the area of triangle ABC:
Ratio=Area of △PDCArea of △ABC=X32X=13×12=16
Thus, the final answer is:
ar(ΔPDC):ar(ΔABC)=1:6
Area of △ADP=23×X=2X3
Area of △ADC=Area of △ADP+Area of △PDC
Therefore, we can express the area of triangle PDC as:
Area of △PDC=Area of △ADC−Area of △ADP
Substituting the values we have:
Area of △PDC=X−2X3=3X3−2X3=X3
Area of △ABC=Area of △ABD+Area of △ACD=X+X=2X
Ratio=Area of △PDCArea of △ABC=X32X=13×12=16
ar(ΔPDC):ar(ΔABC)=1:6
Topper's Solved these Questions
- SOF INTERNATIONAL MATHEMATICS OLYMPIADBook:SCIENCE OLYMPIAD FOUNDATION Chapter:SOF INTERNATIONAL MATHEMATICS OLYMPIADExercise:EVERYDAY MATHEMATICS
Explore 10 Videos
- SOF INTERNATIONAL MATHEMATICS OLYMPIADBook:SCIENCE OLYMPIAD FOUNDATION Chapter:SOF INTERNATIONAL MATHEMATICS OLYMPIADExercise:ACHIEVERS SECTION
Explore 5 Videos
- SOF INTERNATIONAL MATHEMATICS OLYMPIADBook:SCIENCE OLYMPIAD FOUNDATION Chapter:SOF INTERNATIONAL MATHEMATICS OLYMPIADExercise:ACHIEVERS SECTION
Explore 5 Videos
- QUADRILATERALSBook:SCIENCE OLYMPIAD FOUNDATION Chapter:QUADRILATERALSExercise:Achievers Section (HOTS)
Explore 3 Videos
- STATISTICSBook:SCIENCE OLYMPIAD FOUNDATION Chapter:STATISTICSExercise:Achievers Section (HOTS)
Explore 3 Videos
Similar Questions
A hemispherical dome of builiding needs to be painted from outside . If the circumference of the base of the dome is 17.6 m, then find the cost of painiting it at the rate of Rs 8 per 100cm2.
View SolutionRead the statements carefully and select the correct option .
Statement - I : If diagonals of a cyclic quadrilateral are diameter of the circle through the vertices of the quadrilateral, then it is a rectangle .
Statement - II : If the sum of a pair of opposite angles of a quadrilateral is 180∘ , then the quadrilateral is cyclic .
View SolutionRead the statements carefully and select the correct option .
Statement - I : If diagonals of a cyclic quadrilateral are diameter of the circle through the vertices of the quadrilateral, then it is a rectangle .
Statement - II : If the sum of a pair of opposite angles of a quadrilateral is 180∘ , then the quadrilateral is cyclic .
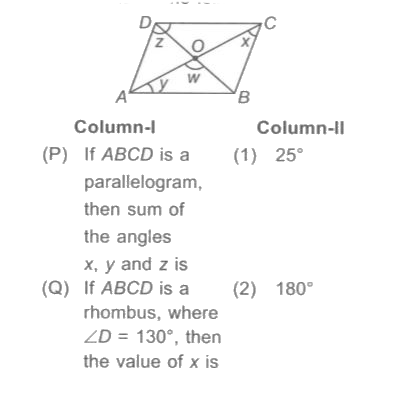
View SolutionBy using a given figure of quadrilateral ABCD, match the following:

View SolutionState 'T' for true and 'F' for false.
(i) If the number of observation is even then the median is mean of (n2)thand(n2+1)th terms
(ii) After four vertical lines for a tally marks, if the tally marks occurs for the fifth time, then the fifth line is put vertically with previous four lines.
(iii) If the range of the data with minimum value 16, is 87, then the maximum value is 71.
(iv) Mode of the data 14, 71, 51, 91, 15, 2, 15, 51, 19, 41, 51, 15, 51, is 51
(v) Mean of first ten natural numbers is 5.5
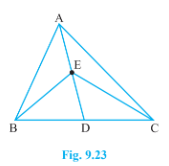
View SolutionIn Fig.9.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE).
View SolutionIn the adjoining figure,E is a point on the median AD of a Delta ABC. Show that ar (Delta ABE)=(Delta ACE)
View SolutionThe base BC of Delta ABC is divided at D, so that BD=(1)/(2)DC. Prove that ar(Delta ABD)=(1)/(3)ar(Delta ABC)
View SolutionIn Delta ABC,AD and BE are altitudes.Prove that (ar(Delta DEC))/(ar(Delta ABC))=(DC^(2))/(AC^(2))
View SolutionIt is given that ΔABC~ΔPRQandBCQR=23 then ar(ΔPQR)ar(ΔABC)=?
View SolutionIn an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?

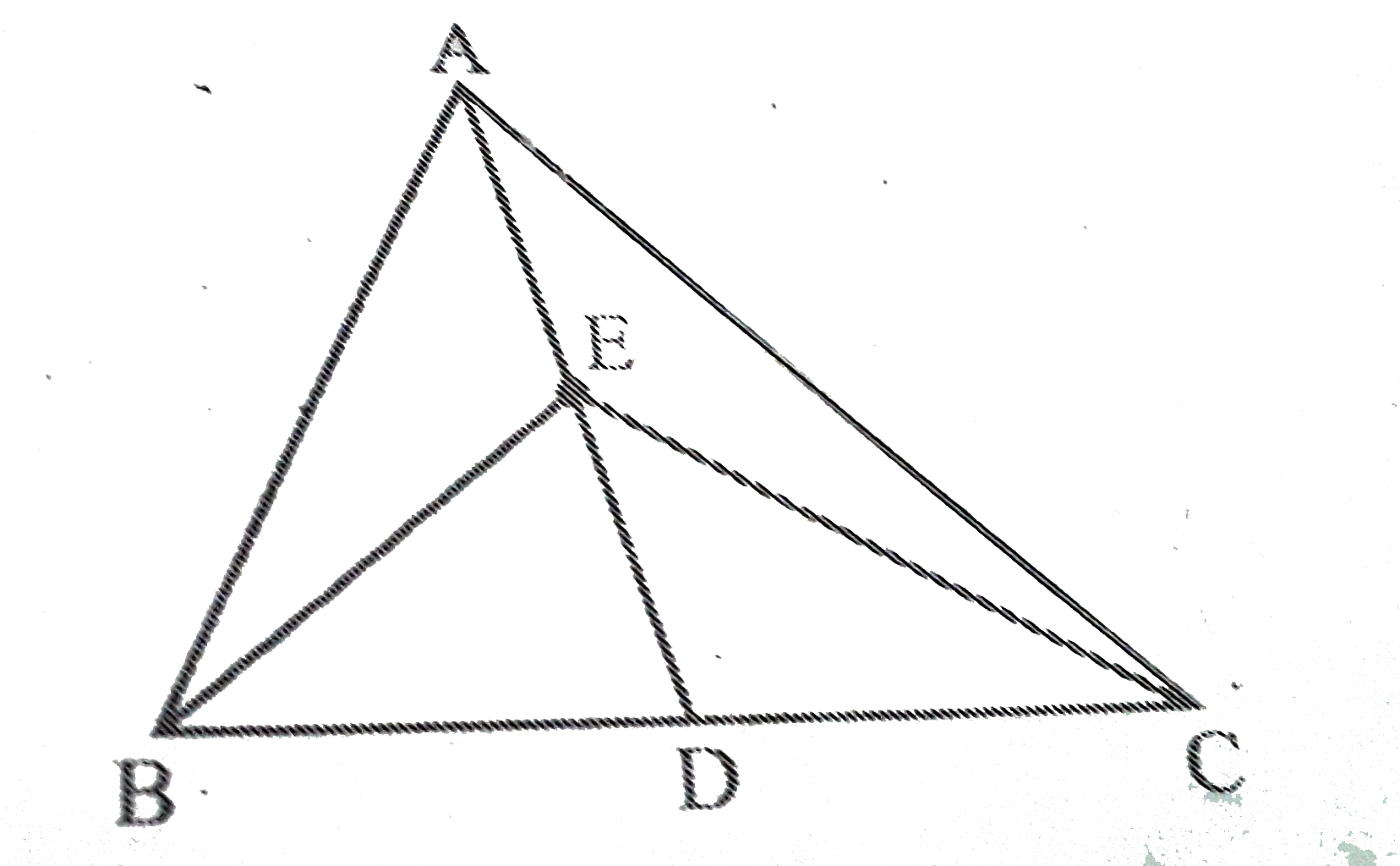
View Solutionआकृति में, ΔABC की एक मध्यिका AD पर स्थित E कोई बिंदु है दर्शाइए कि ar(ABE)=ar(ACE) है।
View Solutionत्रिभुज ABC की AD एक माध्यिका है तथा भुजा AC पर बिंदु P इस प्रकार है कि
ar(ΔADP):ar(ΔABD)=2:3, तो ar(ΔPDC):ar(ΔABC)
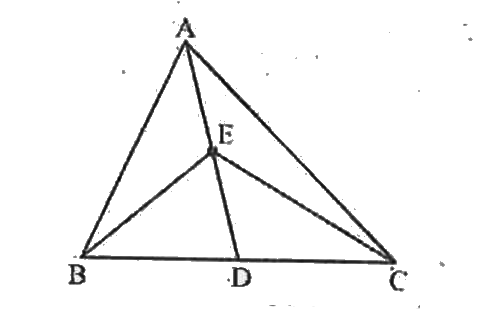
View SolutionIn the figure 11.23, E is any point on median AD of a ΔABC. Show that ar (ABE) = ar (ACE).
View SolutionIn the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
View SolutionIn the Given figure, E is any point on median AD of a △ABC Show that ar (ABE) = ar (ACE)
View Solution
