Two small conducting balls A and B of radius r1 and r2 have charges q1 and q2 respectively. They are connected by a wire.Obtain the expression for charges on A and B, in equilibrium.
To find the expression for the charges on conducting balls A and B in equilibrium, we need to follow these steps:
1. Identify the given parameters:
- Radius of ball A: r1
- Radius of ball B: r2
- Initial charges on ball A: q1
- Initial charges on ball B: q2
2. Understand the equilibrium condition:
When two conducting balls are connected by a wire, they will share charges until they reach the same electric potential. This means the potential V on both balls will be equal.
3. Write the expression for the potential of each ball:
The potential V of a charged sphere is given by:
V=q4πϵ0r
where q is the charge and r is the radius of the sphere.
For ball A:
VA=qA4πϵ0r1
For ball B:
VB=qB4πϵ0r2
4. Set the potentials equal to each other:
Since VA=VB in equilibrium:
qA4πϵ0r1=qB4πϵ0r2
5. Simplify the equation:
qAr1=qBr2
qAr2=qBr1
qAqB=r2r1
6. Express the total charge:
Let Q be the total charge:
Q=qA+qB
7. Solve for qA and qB:
From the ratio qAqB=r2r1, we can write:
qA=r2r1qB
Substitute qA in the total charge equation:
Q=r2r1qB+qB
Q=qB(r2r1+1)
qB=Qr2r1+1
qB=Qr2+r1r1
qB=Qr1r1+r2
Now, substitute qB back into the expression for qA:
qA=r2r1qB
qA=r2r1⋅Qr1r1+r2
qA=Qr2r1+r2
Final Expressions:
- Charge on ball A:
qA=Qr2r1+r2
- Charge on ball B:
qB=Qr1r1+r2
- Radius of ball A: r1
- Radius of ball B: r2
- Initial charges on ball A: q1
- Initial charges on ball B: q2
When two conducting balls are connected by a wire, they will share charges until they reach the same electric potential. This means the potential V on both balls will be equal.
The potential V of a charged sphere is given by:
V=q4πϵ0r
where q is the charge and r is the radius of the sphere.
VA=qA4πϵ0r1
VB=qB4πϵ0r2
Since VA=VB in equilibrium:
qA4πϵ0r1=qB4πϵ0r2
qAr1=qBr2
qAr2=qBr1
qAqB=r2r1
Let Q be the total charge:
Q=qA+qB
From the ratio qAqB=r2r1, we can write:
qA=r2r1qB
Q=r2r1qB+qB
Q=qB(r2r1+1)
qB=Qr2r1+1
qB=Qr2+r1r1
qB=Qr1r1+r2
qA=r2r1qB
qA=r2r1⋅Qr1r1+r2
qA=Qr2r1+r2
- Charge on ball A:
qA=Qr2r1+r2
qB=Qr1r1+r2
Topper's Solved these Questions
Similar Questions
Two charged spheres A and B having their radii in the ratio 1 : 2 are connected together with a conducting wire. The ratio of their surface charge densities (σAσB) will be :
View SolutionUsing Gauss’s law, derive expression for intensity of electric field at any point near the infinitely long straight uniformly charged wire.
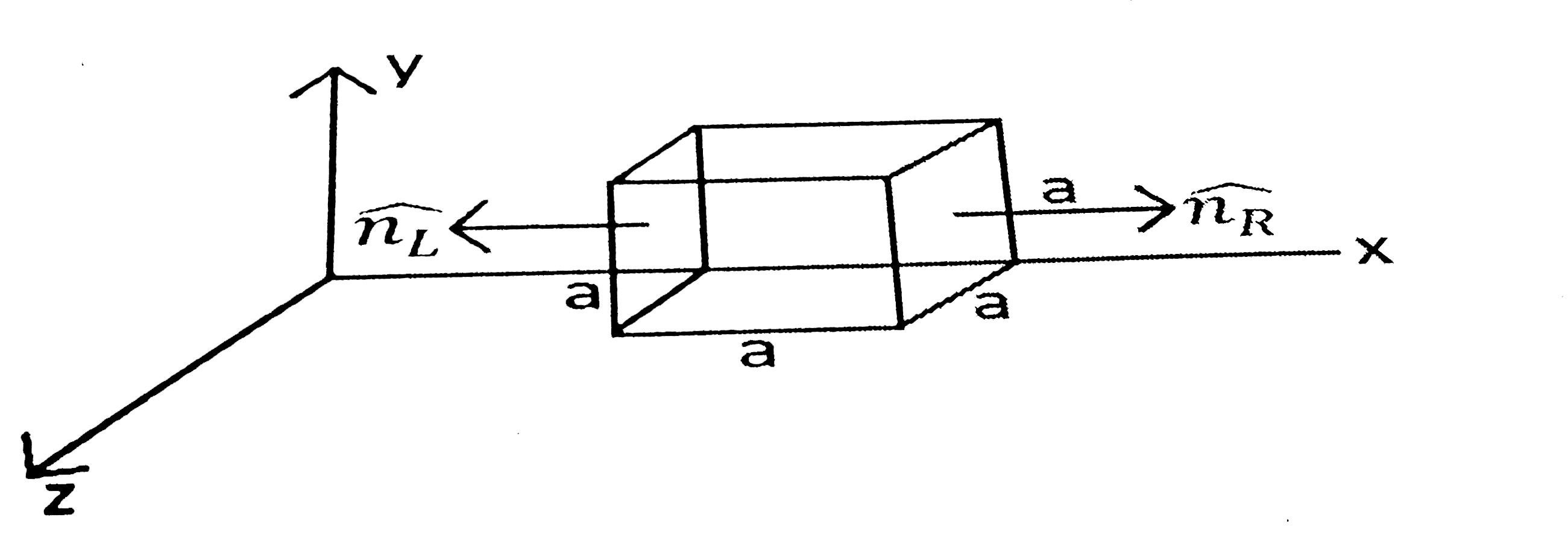
The electric field components in the following figure are Ex=αx,Ey=0,Ez=0, in which α=400N/C m. Calculate (i) the electric flux through the cube, and (ii) the charge within the cube assume that a = 0.1m.
View SolutionA small sphere of radius r1 and charge q1 is enclosed by a spherical shell of radium r2 and charge q2. Show that if q1 is positive , charge will neecessarily flow from the sphere to the shell ( when the two are connected by a wire ) no matter what the charge q2 on the shell is .
View SolutionDeduce an expression for the potential energy of a system of two point charges q_1 and q_2 located at positions r_1 and r_2 respectively in an external field (vecE)
View SolutionA small sphere of radius r1 and charge q1 is enclosed by a spherical shell of radius r2 and charge q2. Show that if q1 is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q2, on the shell is.

View Solutionत्रिज्या r1 एवं r2 के दो चालक गोले समान रूप से आवेशित हैं। उनके विभव का अनुपात होगा
View Solutionq1 एवं q2 आवेशों वाले त्रिज्या R1 एवं R2 के दो विद्युतरोधी आवेशित गोले क्रमशः एक-दूसरे से जुड़े हैं, तो
View Solutionत्रिज्या r1 एवं आवेश q1 का कोई छोटा गोला त्रिज्या r2 आवेश q2 एवं के किसी गोलीय कवच द्वारा घिरा हुआ है। यदि q1 धनात्मक है, तो
View SolutionA small sphere of radius r_1 and charge q_1 is enclosed by a spherical shell of radius r_2 and charge q_2 . Show that if q_1 is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q_2 on the shell is.
View SolutionWrite the vector form of force acting between two charges q_1 and q_2 having vec r_1 and vec r_2 as their position vectors respectively.
View SolutionTwo concentric thin metallic spheres of radii R_1 and R_2 (R_1 gt R_2) bear charges Q_1 and Q_2 respectively. Then the potential at radius r between R_1 and R_2 will be (k =1//4 pi in_0)
View SolutionTwo conducting spheres of radius r1 and r2 are equally charged. The ratio of their intensities will be :
View SolutionTwo insulated spheres of radii R_1 and R_2 having changes Q_1 and Q_2 respectively are connected to each other. There is:
View SolutionThree electric point charges q0,q1 and q2 are at distances →tr0,→r1 and →r2 respectively with respect to same origin. What is the force on charge q0 in the filed of charges q1 and q2 ?
View SolutionN identical oil drops each of capacity C1 are charged to potential V1. Each drop has radius R1 and have charge Q1. All the N-drops coalesce to form a larger drop of radius R2 charge Q2 potential V2 and capacity C2. Then (R2R1) and (Q2Q1) respectively are
View SolutionA small sphere of radius r1 and charge q1 is enclosed by a spherical shell of radius r2 and charge q2. Show that if q1 is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge q2 on the shell is.
View Solution

