त्रिज्या R की एक अचालक चकती के पृष्ठ पर आवेश Q एकसमान रूप से वितरित किया गया है। चकती कोणीय वेग ω से इसके तल के लंबवत तथा केंद्र से गुजरने वाली अक्ष के पारित : घूर्णन करती है। इस घूर्णन के परिणमास्वरूप चकती के केंद्र पर चुंबकीय क्षेत्र B प्राप्त होता है । यदि हम चकती पर रखे गए आवेश तथा इसके कोणीय वेग को नियत रखे तथा चकती की त्रिज्या में परिवर्तन करे, तो चकती के केंद्र पर चुंबकीय क्षेत्र का विचरण (variation) किस चित्र द्वारा दर्शाया जायेगा?
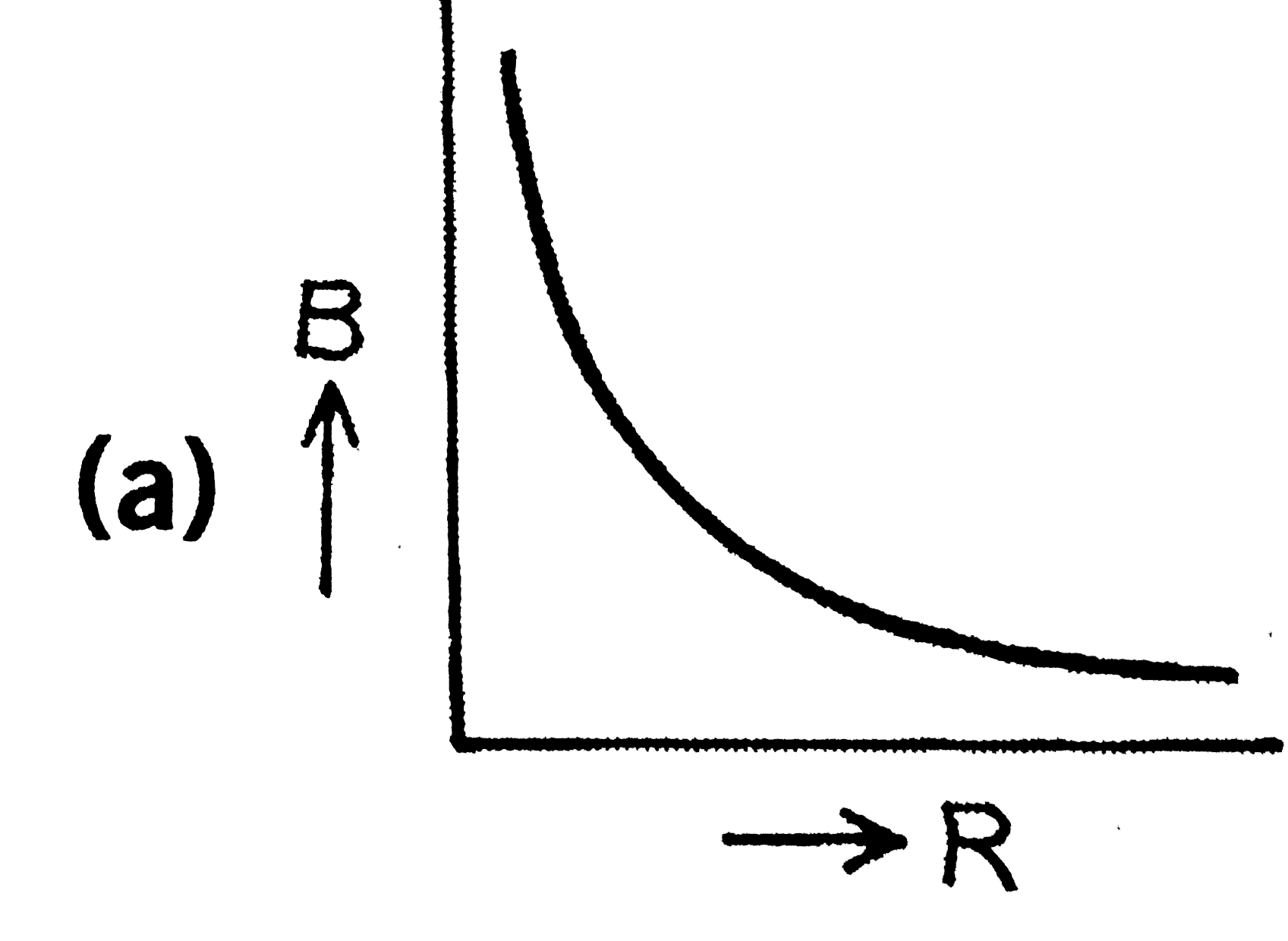
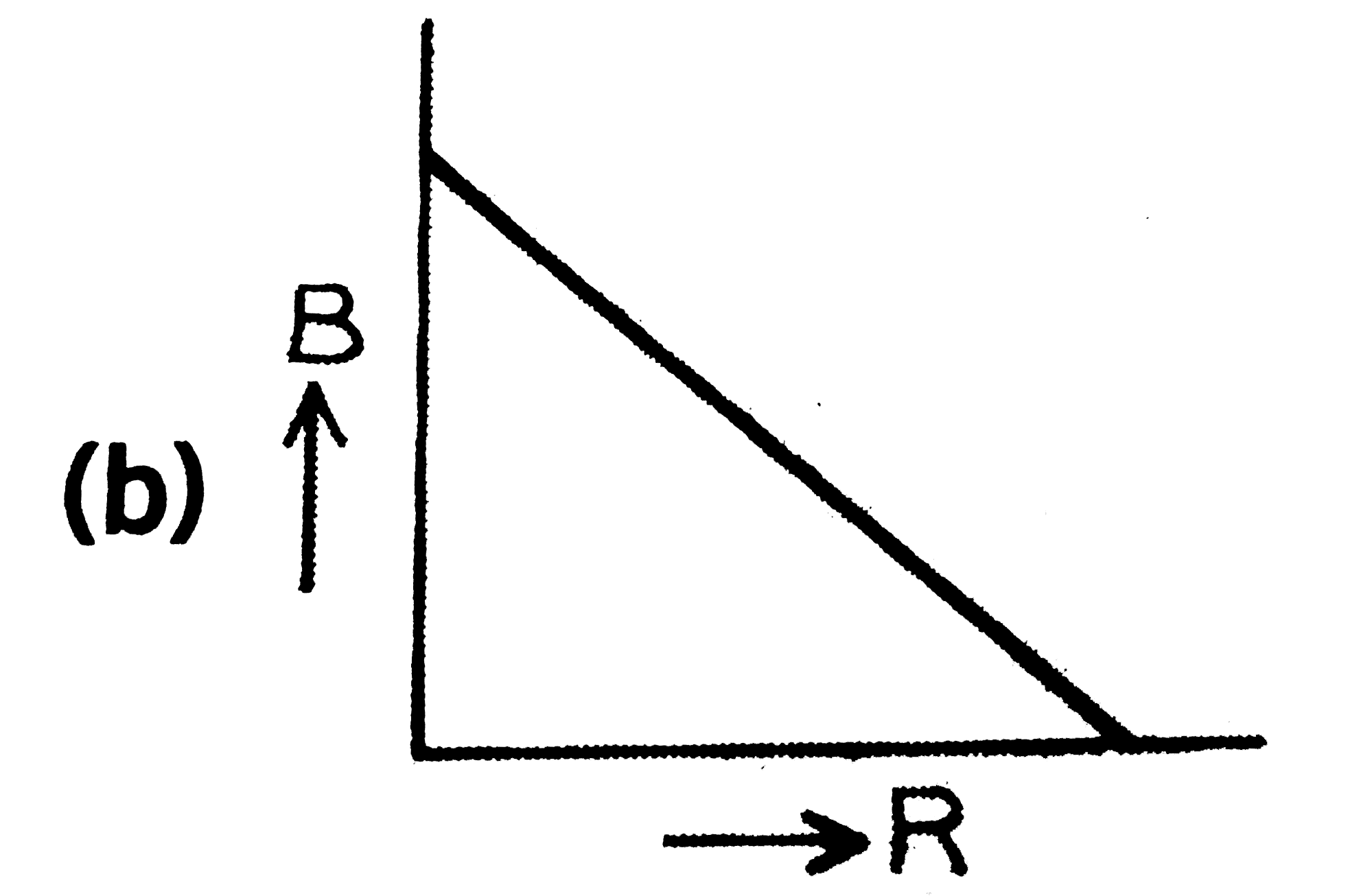
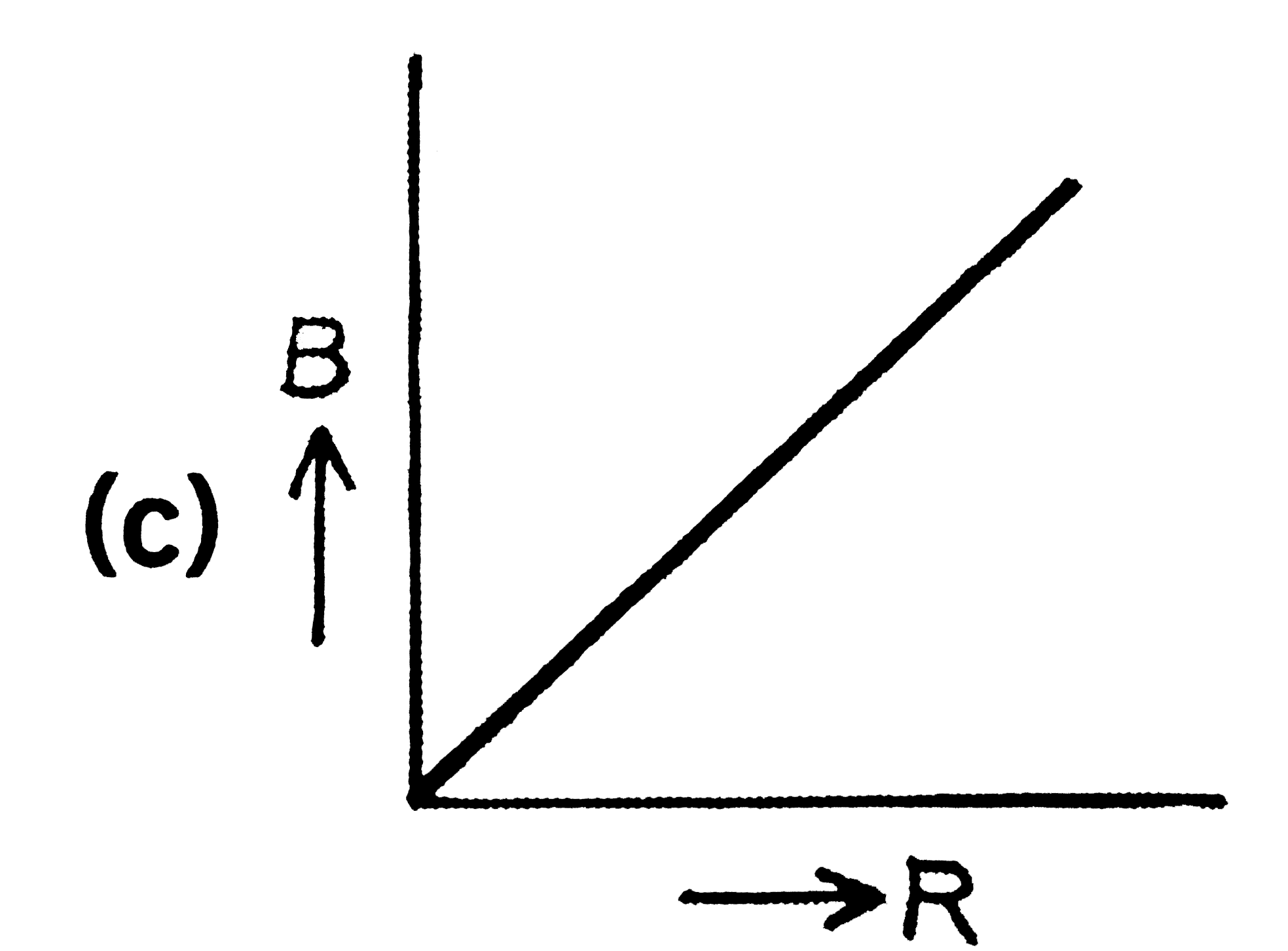
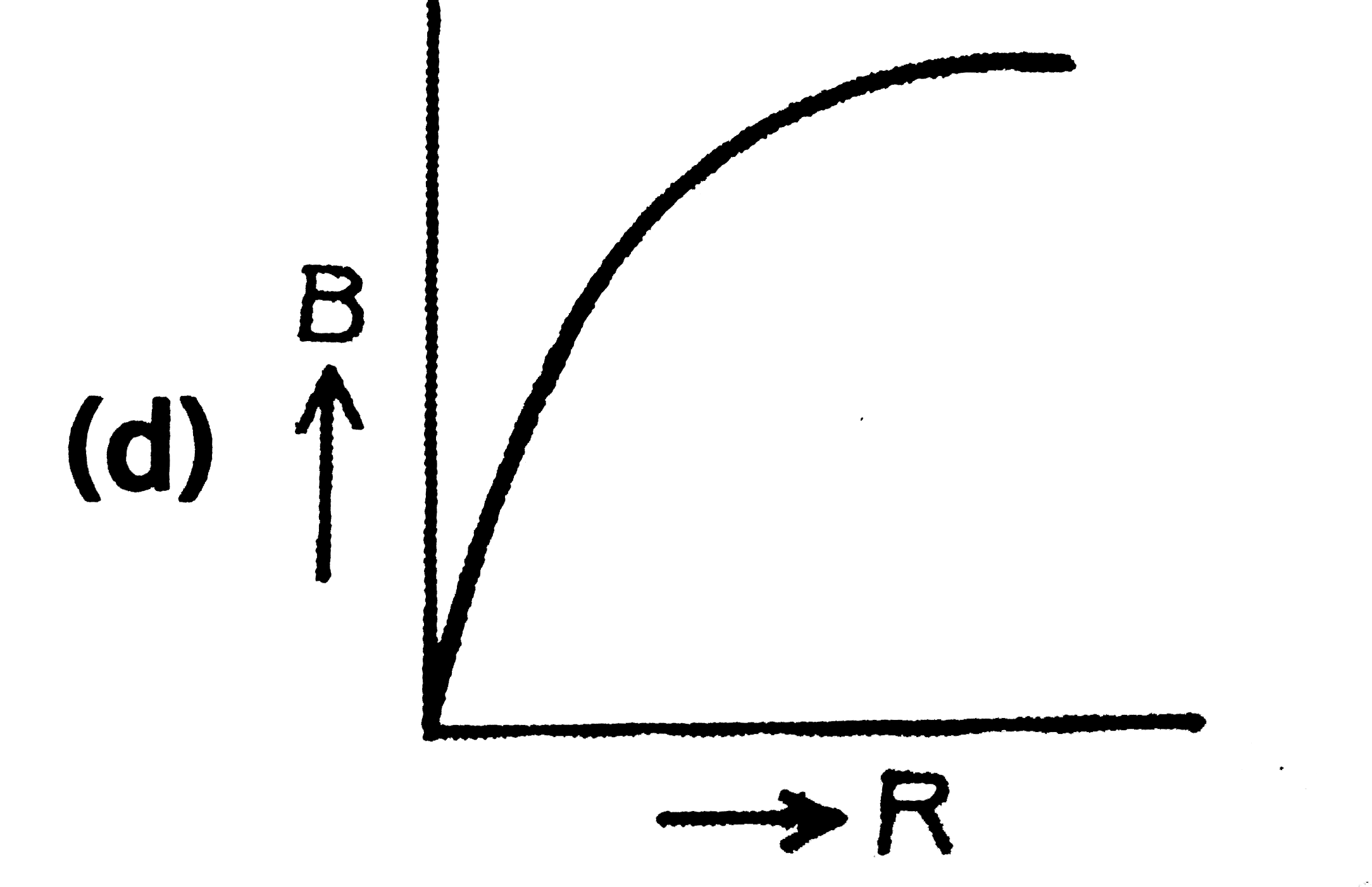
The correct Answer is:A
चकती के आवेश का पृष्ठ-घनत्व σ=QπR2 माना चकती अनेक वलयों से मिलकर बनी है, एक वलय जिसकी त्रिज्य r मोटाई dr है, पर आवेश dQ=2πrdrσ । इस वलय के केंद्र पर चुंबकीय क्षेत्र
dB=μ0i2r=μ02rdQdt=μ02r(2πrdrσ)×ω2π=μ0σω2dr
∴B=∫R0μ0σω2dr=μ0ω2×QπR2×R=μ0Qω2πR
अथवा B∝1R चित्र (a) यह सम्बन्ध व्यक्त करता है।
टॉपर्स ने हल किए ये सवाल
- गतिमान आवेश तथा चुंबकीय क्षेत्र Book:NOOTAN HINDIChapter:गतिमान आवेश तथा चुंबकीय क्षेत्र Exercise:आंकिक
Explore 54 Videos
- कॉलम का नियम तथा वैद्युत क्षेत्र Book:NOOTAN HINDIChapter:कॉलम का नियम तथा वैद्युत क्षेत्र Exercise:वस्तुनिष्ठ प्रकार प्रश्न
Explore 16 Videos
- चल कुण्डली धारामापी Book:NOOTAN HINDIChapter:चल कुण्डली धारामापी Exercise:वस्तुनिष्ठ प्रकार प्रश्न
Explore 15 Videos
समान प्रश्न
एक समतल वृताकार कुंडली में 100 फेरे है। तथा उसकी त्रिज्या 3.0 सेमी है। इस कुण्डली में 2.0 ऐम्पियर की धारा प्रवाहित की जाती है । कुण्डली के अक्ष पर स्थित कुण्डली के केंद्र से 4.0 सेमी दुरी पर स्थित बिंदु पर चुंबकीय क्षेत्र की गणना कीजिए।
View Solutionकल्पना कीजिए कि एक प्रोटॉन और एक इलेक्ट्रॉन के आवेश में अल्प अंतर होता है। इनमे से एक −e है और दूसरा(e×Δe) है। यदि एक दूसरे से 'd' दूरी पर रखे हाइड्रोजन के दो परमाणुओं के बीच (जहाँ d परमाणु के साइज से बहुत अधिक है) स्थिर वैद्युत बल और गुरुत्वीय बल का परिणामी (नैट) शून्य है तो Δe कि कोटि होगी: (दिया है हाइड्रोजन का द्रव्यमान mh=1.67×10−27kg)
View Solutionआरेख में दण्ड (छड़) चुम्बको की व्यवस्थाओं के विन्यास दर्शाये गये है। प्रत्येक चुम्बक की द्विध्रुव आघूर्ण →M है। किस विन्यास में नेट चुम्बकीय द्विध्रुव आघूर्ण का मान अधिकतम होगा?

View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये ।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?
View Solutionएकसमान विद्युत क्षेत्र E=3×103ˆi(N)/C पर विचार कीजिये।
(a) इस क्षेत्र का 10 cm भुजा के वर्ग के उस पार्श्व से जिसका तल yz तल के समांतर है, गुजरने वाला फ्लक्स क्या है ?
(b) इस वर्ग से गुजरने वाला फ्लक्स कितना है यदि इसके तल का अभिलंब x- अक्ष से 60∘ कोण बनता है ?
एकसमान विद्युत क्षेत्र का 20 cm भुजा के किसी घन से (जो इस प्रकार अभिविन्यासित है की उसके फलक निर्देशांक तलों के समांतर है ) कितना नेट फ्लक्स गुजरेगा ?
View Solutionकिसी बिंदु आवेश के कारण उस बिंदु को केंद्र मानकर खींचे गए 10cm त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स −1.0×103Nm2/C त्रिज्या के गोलीय गॉऊसीय पृष्ठ पर विद्युत से फ्लक्स। (a) यदि गॉऊसीय पृष्ठ की त्रिज्या दो गुनी कर दी जाए तो पृष्ठ से कितना फ्लक्स गुजरेंगा ? (b) बिंदु आवेश का मान क्या है।
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionएक अतिपरवलय का केंद्र मूलबिंदु पर है तथा यह बिन्दु (4,2) से होकर जाता है और इसका अनुप्रस्थ (transverse) अक्ष X-अक्ष के अनुदिश है जिसकी लम्बाई 4 है तो इस अतिपरवलय की उत्केन्द्रता (eccentricity) है
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionयदि R त्रिज्या का एक वृत्त मूलबिंदु O से होकर जाता है तथा निर्देशांक अक्षो को A और B पर कट्टा है , तो O से रेखा AB पर डाले गए लम्ब के पाद का बिन्दुपथ है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View Solutionधारावाहिक चाप के कारण चुंबकीय क्षेत्र|वृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionवृत्ताकार पथ पर आवेश की गति के कारण केंद्र पर चुंबकीय क्षेत्र|धारावाहि चाप के कारण केंद्र पर चुंबकीय क्षेत्र
View Solutionएक 5 kg द्रव्यमान वाली वस्तु पर 2s के लिये एक नियत बल कार्यरत होता है। यह वस्तु के वेग को 3m/s से बढा 7m/s कर देता है। लगाये गये बल की मात्रा ज्ञात करें
View Solution
