The range of a for which the equation x2+ax−4=0 has its smaller root in the interval (−1,2) is
(−∞,−3)
(0, 3)
(0,∞)
(−∞,−3)∪(0,∞)
The correct Answer is:A
Clearly , f(−1)>0,f(2)<0
Now ,
f(0)=−4<0
⇒f(−1)=1−a−4>0
and f(2)=4+2a−4<0
⇒a<−3anda<0
⇒a∈(−∞),−3)
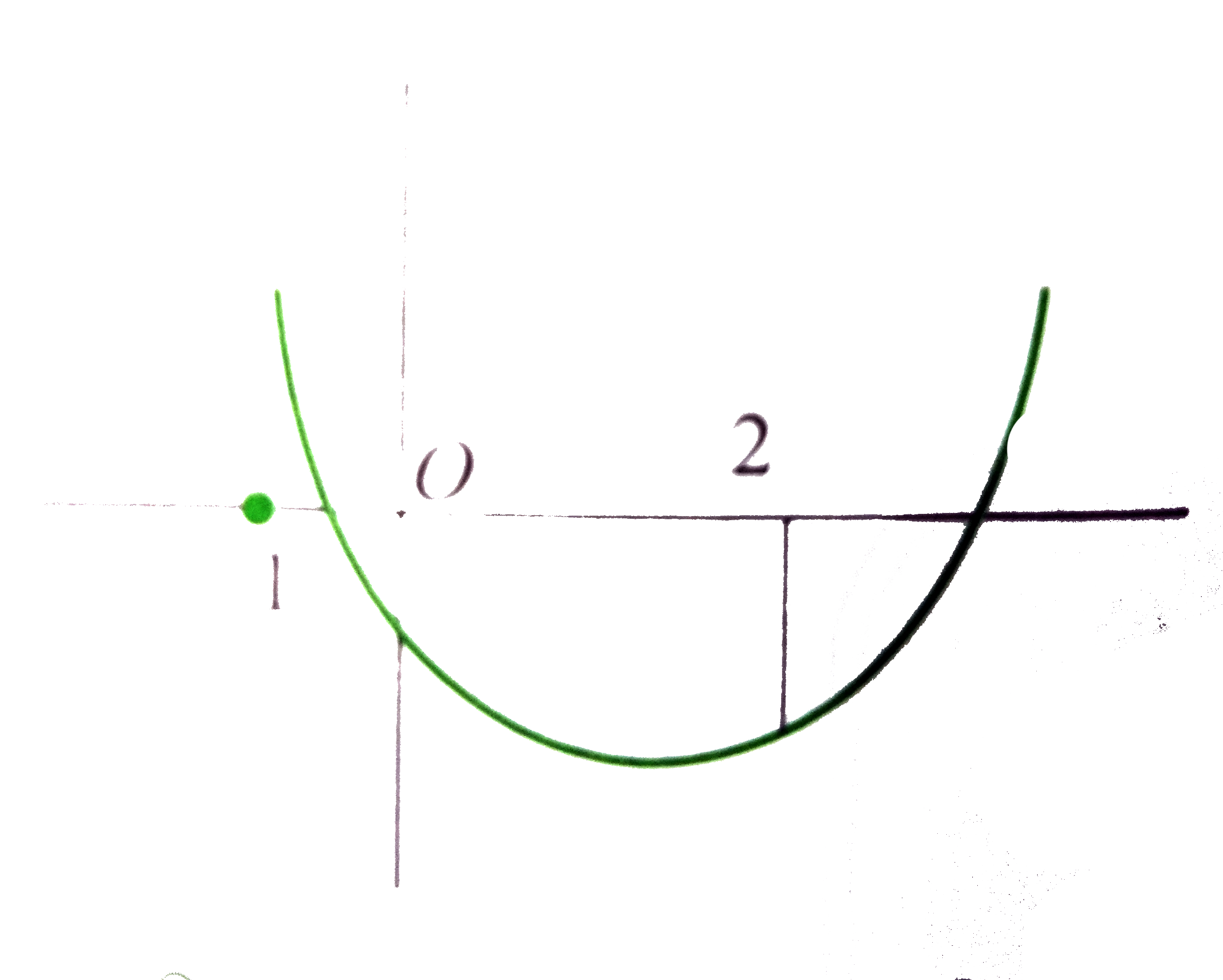
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Multiple)
38 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Comprehension)
37 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise 2.13
9 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year
4 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGECHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - Question Bank
20 Videos
Similar Questions
if c≠0 and the equation p2x=ax+c+bx−c has two equal roots, then p can be
View SolutionConsider an unknow polynomial which divided by (x−3) and (x−4) leaves remainder 2 and 1, respectively. Let R(x) be the remainder when this polynomial is divided by (x−3)(x−4).
If equations R(x)=x2+ax+1 has two distint real roots, then exhaustive values of a are.
View SolutionFind the values of a if x2−2(a−1)x+(2a+1)=0 has positive roots.
View SolutionThe locus of the orthocentre of the triangle formed by the lines (1+p)x−py+p(1+p)=0,(1+q)x−qy+q(1+q)=0 and y = 0, where p≠⋅q, is (A) a hyperbola (B) a parabola (C) an ellipse (D) a straight line
View SolutionLet the line L1:x−12=y−23=z−34 and L2:x−21=y−32=z−k4 intersect at P.The least distance of P from the plane 3x−4y−12z+4=0, equals
View SolutionThe range of a for which the equation x2+ax−4=0 has its smaller root in the interval (−1,2)is a. (−∞,−3) b. (0,3) c. (0,∞) d. (−∞,−3)∪(0,∞)
View SolutionIf both the roots of x2+ax+2=0 lies in the interval (0, 3), then find the exhaustive range of value of a.
View SolutionIf alpha,beta are the roots of the equation x^(2)-2mx+m^(2)-(1)/(4)=0 then the range of values of m for which alpha,beta in(-1,2) is
View Solutionif the equation x^(2)+ax+b=0 has one root equal to unity and other root lies between the roots of the equation x^(2)-7x+12=0, then range of values of a belongs to
View SolutionLet x2−(m−3)x+m=0(mεR) be a quadratic equation . Find the values of m for which the roots are (ix)one root is smaller than 2 & other root is greater than 2 (x) both the roots are greater than 2 (xi) both the roots are smaller than 2 (xii)exactly one root lies in the interval (1,2) (xiii) both the roots lies in the interval (1,2) (xiv) atleast one root lies in the interval (1,2) (xv) one root is greater than 2 and the other root is smaller than 1
View Solutionयदि समीकरण x2+ax+12=0 का एक मूल 2 है तथा द्विघात समीकरण x2+ax+q=0 के समान मूल हों, तो q=
View SolutionIf 4 is a root of the equation x2+ax−12=0 , then which of the following is its other root?
View SolutionIf one root of x2+ax+8=0 is 4 and the equation x2+ax+b=0 has equal roots then the value of b=
View Solutionयदि समीकरण x2+ax+12=0 का एक मूल 4 है तथा समीकरण x2+ax+b=0 के मूल समान हैं, तो b का मान होगा
View SolutionThe value of 'a' for which the equation x3+ax+1=0 and x4+ax2+1 =0 has a common root is :
View SolutionFor which values of 'a' so that the equation x2+(3−2a)x+a=0 has exactly one root in the interval (−1,2)
View Solution

