Let the function f(x) be defined as follows:
f(x)=⎧⎪⎨⎪⎩x3+x2−10x−1≤x≤0cosx0≤x≤π/21+sinxπ/2≤x≤π
A
a local minimum at x=π/2
B
a global maximum at x=π/2
C
a absolute maximum at x=-1
D
a absolute maximum at x=π
Video Solution
Text Solution
The correct Answer is:C
Thus the graph of f(x) is
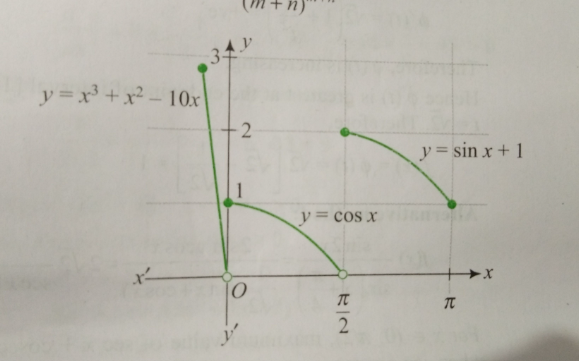
|
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGEChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Exercise (Multiple)
Explore 40 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGEChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Exercise (Comprehension)
Explore 42 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBook:CENGAGEChapter:MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSExercise:Exercise 6.7
Explore 5 Videos
- METHODS OF DIFFERETIATIONBook:CENGAGEChapter:METHODS OF DIFFERETIATIONExercise:Question Bank
Explore 29 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBook:CENGAGEChapter:MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSExercise:Comprehension Type
Explore 6 Videos
Similar Questions
Knowledge Check
Let the function f(x) be defined as follows:
f(x)=⎧⎪⎨⎪⎩x3+x2−10x−1≤x≤0cosx0≤x≤π/21+sinxπ/2≤x≤πAa local minimum at x=π/2Ba global maximum at x=π/2Ca absolute maximum at x=-1Da absolute maximum at x=πLet f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x3+x2−10x−1≤x<0cosx0≤x<π21+sinxπ2≤x≤x Then at x=π2, f(x) has:
Aa local minimumBa local maximumCno extremumDno local maximumLet f(x) = ⎧⎪⎨⎪⎩x3+x2−10x−1≤x<0sinx0≤x<x/21+cosxπ/2≤x≤π then f(x) has
Alocal maximum at x=π2Blocal minimum at x=π2Cabsolute minimum at x=0,πDabsolute maximum at x=π2
If f(x)={x2+10≤x<1−3x+51≤x≤2
View SolutionLet f(x)⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩−2sinx−π≤x≤−π2asinx+b−π2≤x≤π2cosxπ2≤x≤π
View SolutionLet f(x)⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩−2sinx−π≤x≤−π2asinx+b−π2≤x≤π2cosxπ2≤x≤π
View SolutionLet f(x) = ⎧⎪⎨⎪⎩x3+x2−10x−1≤x<0sinx0≤x<x/21+cosxπ/2≤x≤x then f(x) has
View SolutionConsider a function f(x) in [0,2π] defined as :
f(x)=[[sinx]+[cosx]0≤x≤π[sinx]−[cosx]π<x≤2π
where {.} denotes greatest integer function then.
Number of points where f(x) is non-derivable :
View Solution
