The position of an object moving on a straight line is defined by the relation x=t3−2t2−4t, where x is expressed in meter and t in second. Determine
(a) the average velocity during the interval of 1 second to 4 second.
(b) the velocity at t = 1 s and t = 4 s,
(c) the average acceleration during the interval of 1 second to 4 second.
(d) the acceleration at t = 4 s and
(a) The position at t=1s,x1=13−2(1)=−5m
The position at t=4s,x2=43−2(4)2−4(4)=16m
Average velocity in the interval =ΔxΔt=x2−x1Δt
=16−(−5)4−1
=213=7m/s
(b) By the term velocity we mean instantaneous velocity which is given by
v=dxdt=3t2−4t−4
At t=1s,v1=3(1)2−4(1)−4=−5m/s
At t=4s,v2=3(4)2−4(4)−4=28m/s
(c) The average acceleration in an interval is given by
aavg=v2−v1Δt
=(28)−(−5)4−1=333=11m/s2
(d) The instantaneous acceleration is given by
a=dvdt=6t−4
At t=4s,a=6(4)−4=20m/s2
टॉपर्स ने हल किए ये सवाल
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Try Yourself
Explore 40 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - A)
Explore 50 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOVING CHARGE AND MAGNESIUMBook:AAKASH INSTITUTEChapter:MOVING CHARGE AND MAGNESIUMExercise:SECTION D
Explore 16 Videos
समान प्रश्न
The position of a particle moving along a straight line is defined by the relation, x=t3−6t2−15t+40 where x is in meters and t in seconds.The distance travelled by the particle from t=0 to t=2 s is?
View SolutionThe position of a particle varies with time according to the relation x=3t2+5t3+7t, where x is in m and t is in s. Find
(i) Displacement during time interval t = 1 s to t = 3 s.
(ii) Average velocity during time interval 0 - 5 s.
(iii) Instantaneous velocity at t = 0 and t = 5 s.
(iv) Average acceleration during time interval 0 - 5 s.
(v) Acceleration at t = 0 and t = 5 s.
View Solution
ज्ञान जांच
The motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at the origin .A1 , 0 , 4B1 , 4 , 0C10 , 14 , −34D10 , −1 , 0A particle is moving along straight line whose position x at time t is described by x=t3−t2 where x is in meters and tis in seconds . Then the average acceleration from t=2 sec. to t=4 sec, is :
A16m/s2B18m/s2C22m/s2D10m/s2The velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
A0B2 sC3DBoth (1) & (2)
The displacement of a particla moving in straight line is given by s=t4+2t3+3t2+4, where s is in meters and t is in seconds. Find the
(a) velocity at t=1s, (b) acceleration at t=2s,
(c ) average velocity during time interval t=0 to t=2s and
(d) average acceleration during time interval t=0 to t=1s.
View Solution[" 4.If the particle is moving along a straight line "],[" given by the relation "x=2-3t+4t^(3)" where "s" is "],[" in cms.,and "t" in sec.Its average velocity "],[" during the third sec is "]
View SolutionThe v-t graph for a particle moving along x-axis is shown in the figure, find
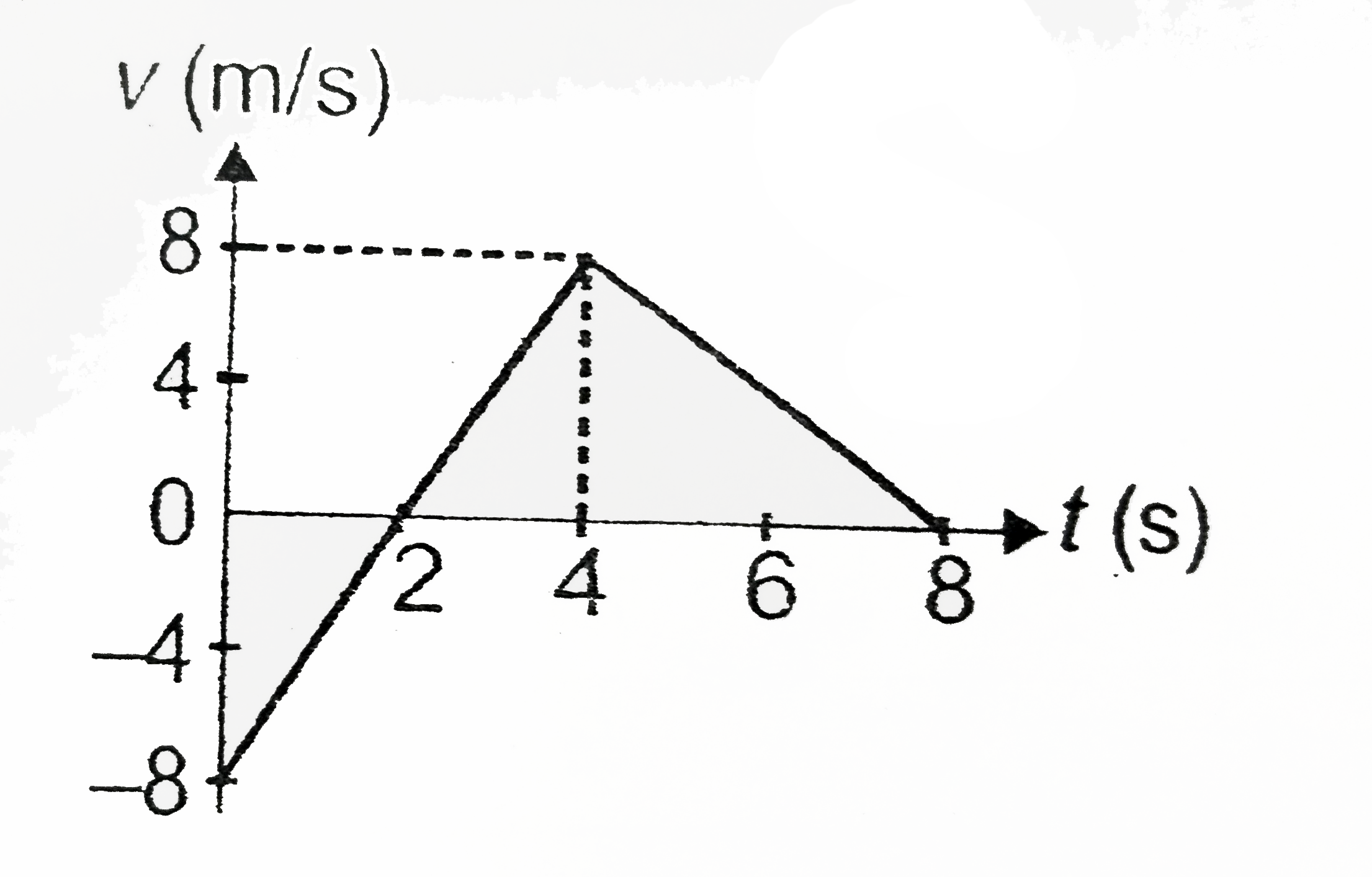
(a) Average velocity in the interval 0 to 8 s.
(b) Average speed in the interval 0 to 8 s.
(c) Average acceleration in the interval 0 to 4 s.
(d) Instantaneous acceleration at t = 2.5 s.
View SolutionThe velocity ofacar travelling on a straight road is given by the equation v=6+8t−t2 where vis in meters per second and t in seconds. The instantaneous acceleration when t=4.5s is :
View SolutionThe displacement of a particle moving in a straight line, is given by s=2t2+2t+4 where s is in metres and t in seconds. The acceleration of the particle is.
View Solution
