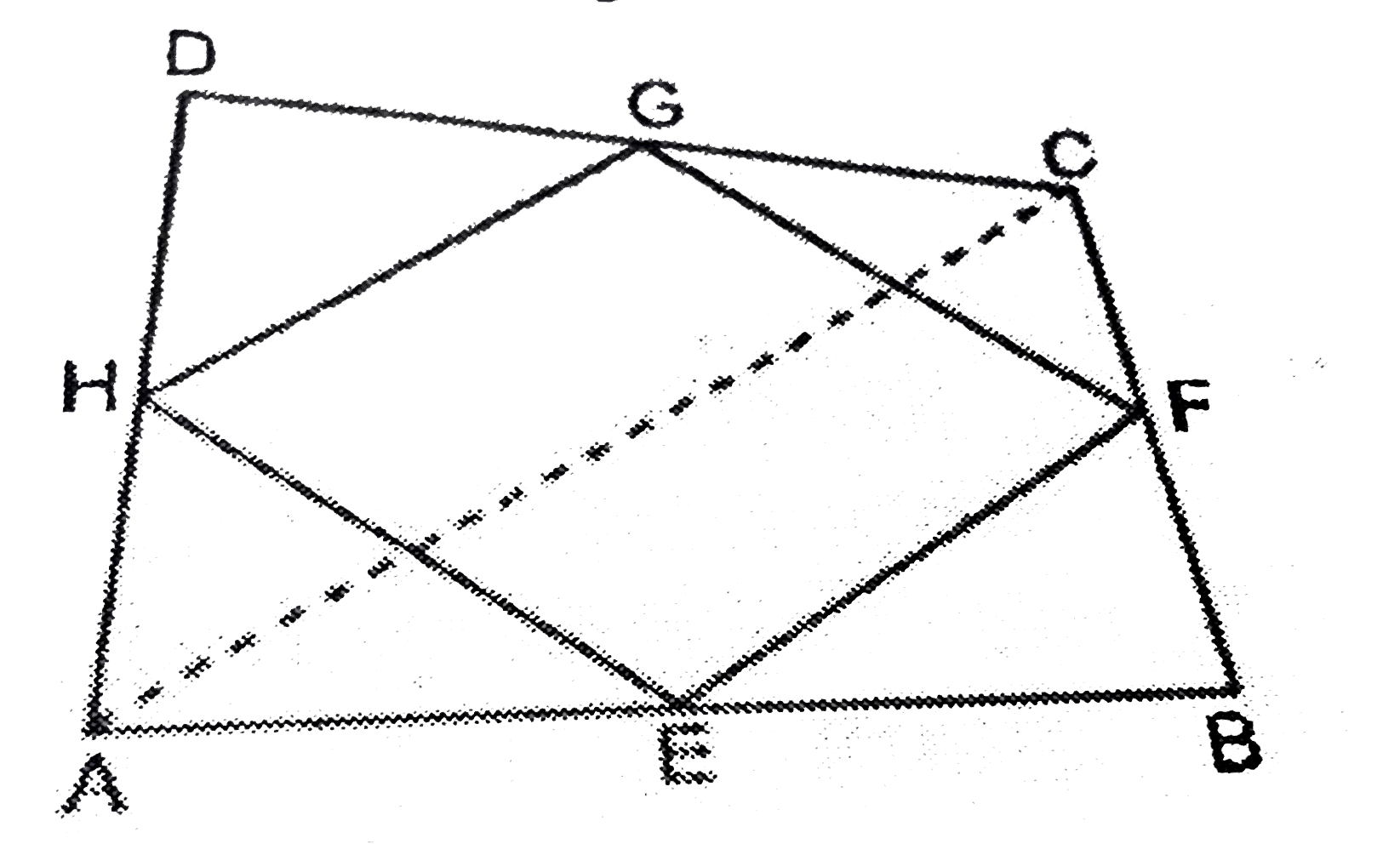
सिद्ध कीजिए कि किसी चतुर्भुज की क्रमिक भुजाओं के मध्य बिंदुओं को मिलाने पर एक समांतर चतुर्भुज बनता है।
ज्ञात है: चतुर्भुज ABCD में E,F,G तथा H भुजाओं AB,BC,CD तथा DA के मध्य बिंदु है।
सिद्ध करना है: EFGH एक समान्तर चतुर्भुज है।
रचना: AC खींचा।
उपपत्ति: ΔABC में E तथा F भुजा AB तथा BC के मध्य बिंदु है।
∴EF∣∣AC…………1
तथा EF=12AC…………..2
[ Δ की दो भुजाओं के मध्य बिंदुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के समांतर तथा उसका आधा होता है।]
इसी प्रकार ΔACD में
∴HG=12AC…………..3
तथा HG∣∣AC…………4
समीकरण 1,2,3 तथा 4 से
EF=HG
और EF∣∣HG…..5
∴EFGH एक समांतर चतुर्भुज है। (सम्मुख भुजाओं के युग्म समांतर तथा समान हैं।)
यही सिद्ध करना था।
टॉपर्स ने हल किए ये सवाल
समान प्रश्न
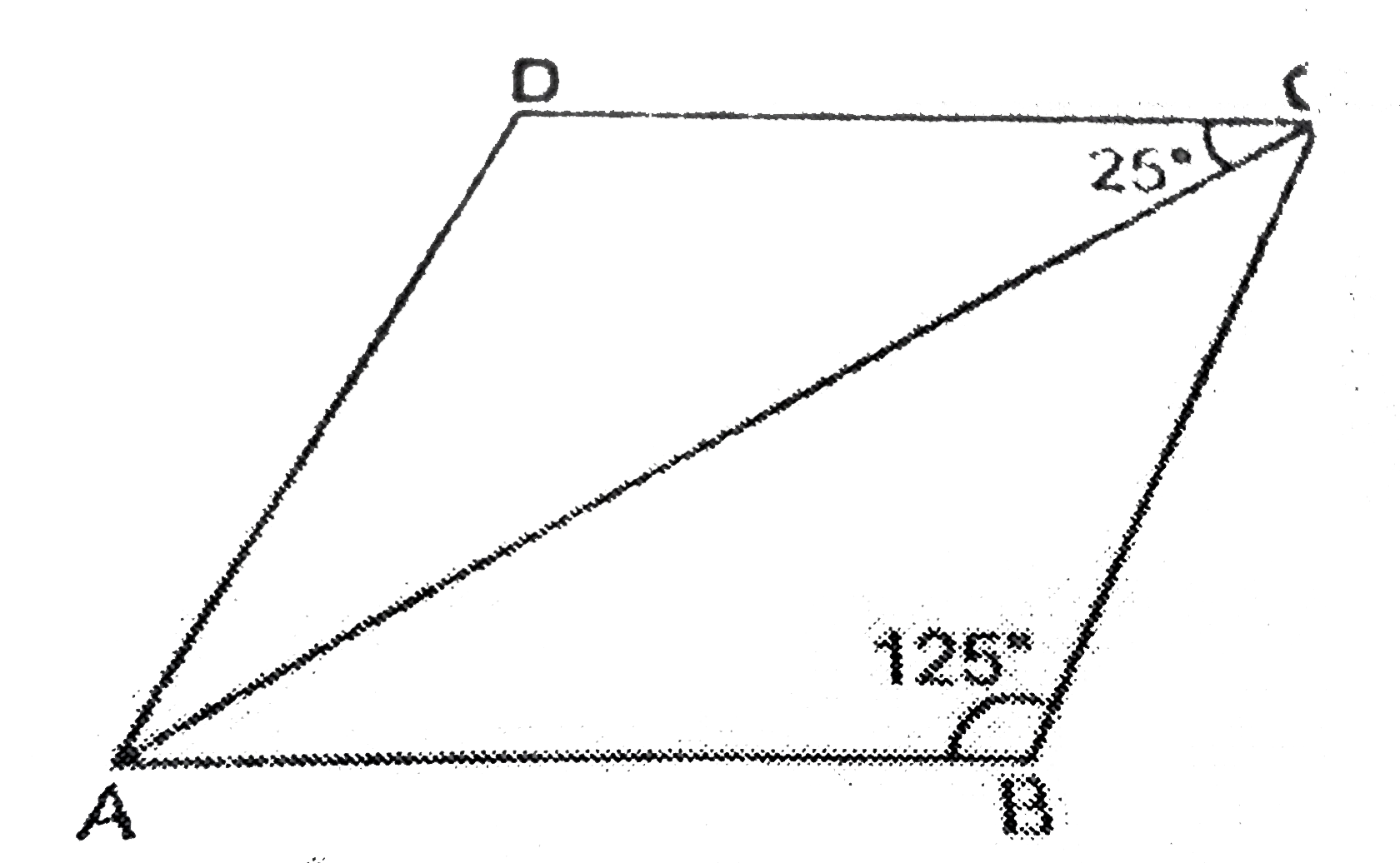
चित्र में ABCD एक समान्तर चतुर्भुज है। यदि ∠ABC=125∘ और ∠DCA=25∘ तो ∠DAC ज्ञात कीजिए।
View Solutionचतुर्भुज ABCD में ∠A=∠C तथा ∠B=∠D हैं। सिद्ध कीजिए ABCD एक समांतर चतुर्भुज है।
View Solutionचित्र में AB>AC है सिद्ध कीजिएः की AB>AD

View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionयदि किसी चतुर्भुज की भुजाओं को क्रमानुसार दिशा व परिमाण में निरूपित करने वाले सदिश ¯a,¯b,¯c,¯d हों तों सिद्ध कीजिए कि चतुर्भुज एक समांतर चतुर्भुज होगा यदि और केवल यदि ¯a+¯c=¯0 जिससे ¯b+¯d=¯0
View Solutionसिद्ध कीजिए कि बिंदुओं (2,3) और(3,4) को मिलाने वाले रेखाखण्ड के मध्य बिंदु के निर्देशांक x और y निम्नलिखित समीकरण को संतुष्ट करते है :
x−y+1=0.
View Solutionपरवलय y2=4px की किसी द्विकोटि की लम्बाई 8p है। सिद्ध कीजिए कि शीर्ष को उसके सिरों से मिलाने वाली सरल रेखाएँ परस्पर लम्ब है।
View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View SolutionRevision|समांतर चतुर्भुज के गुण
View SolutionRevision|चतुर्भुज#!#समांतर चतुर्भुज#!#प्रमेय पर आधारित महत्वपूर्ण प्रश्न
View SolutionThe length of two sides of a parallelogram are 3cm and 10 cm. What is the sum of the squares of diagonals of the parallelogram ? एक समांतर चतुर्भुज के दो भुजाओं की लंबाई 3 सेमी और 10 सेमी है। समांतर चतुर्भुज के विकर्णों के वर्गों का योग क्या होगा ?
View Solutionचतुर्भुज |चतुर्भुज का कोण योग गुण |चतुर्भुज के प्रकार |समांतर चतुर्भुज के गुण|प्रमेय|सारांश
View Solutionसमांतर चतुर्भुज के क्षेत्रफल पर आधारित महत्वपूर्ण प्रश्न
View Solutionसमांतर चतुर्भुज पर आधारित महत्वपूर्ण प्रश्न
View Solutionसमांतर चतुर्भुज के गुण
View Solutionसमांतर चतुर्भुज के गुण#!#NCERT प्रश्नावली 8.1 प्रश्नों पर चर्चा
View Solution
