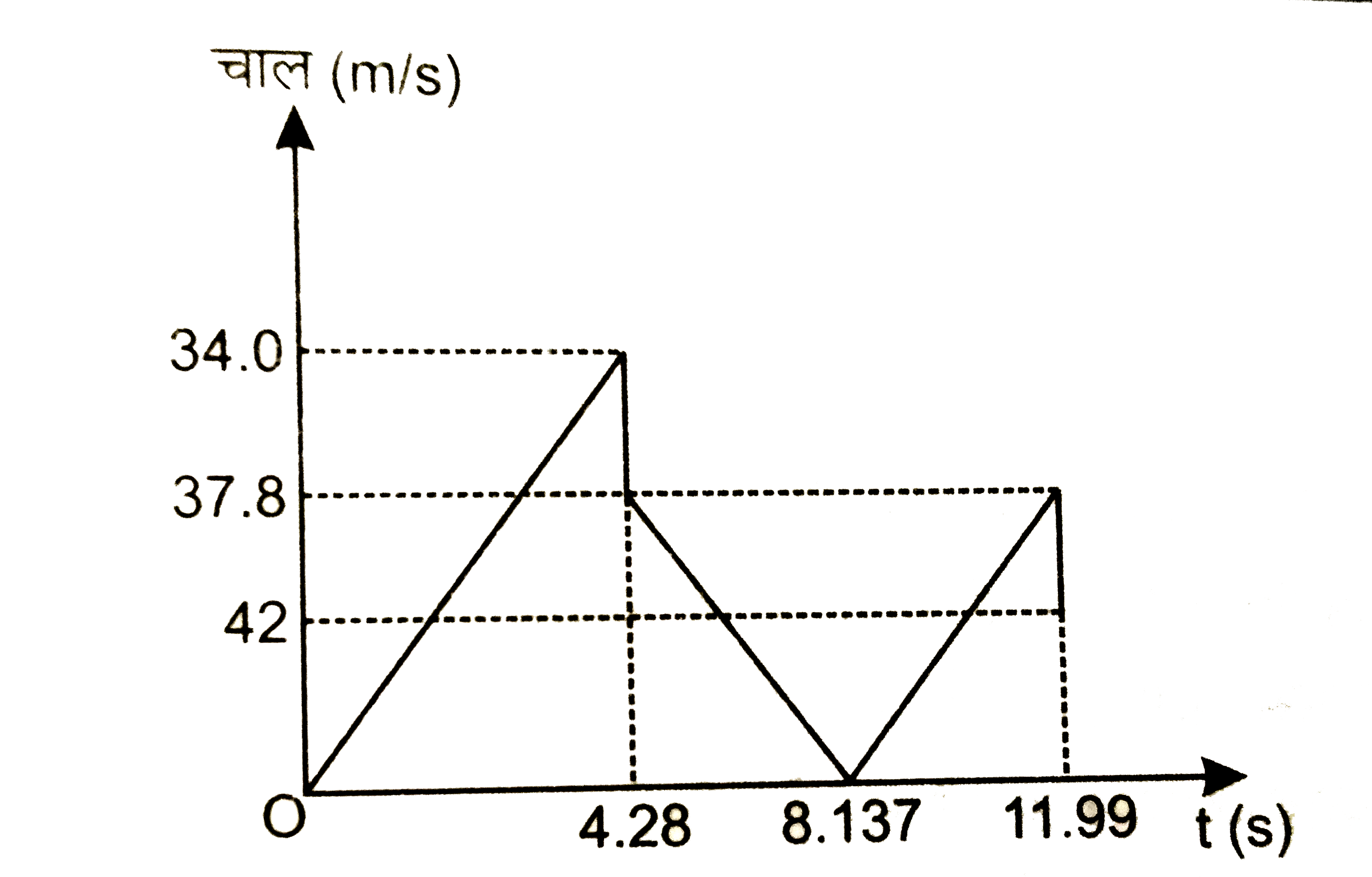
किसी गेंद को 90 मीटर की ऊंचाई से फर्श पर गिराया जाता है फर्श के साथ प्रत्येक टक्कर में गेंद की चाल 1/10 कम हो जाती है। इसकी गति का t=0 से 12s के बीच चाल समय ग्राफ खींचिए।
गेंद का प्रारम्भिक वेग (u)=0
उस बिंदु की ऊंचाई जहां से गेंद गिराई जाती है h=90m
त्वरण g=9.8m/s2
गति के समीकरण से v2=u2+2gh
v2=(0)2+2×9.8×90
(गेंद को विरामावस्था से गिराया जाता है अतः इसका प्रारम्भिक वेग शून्य है)
v=√2×9.8×90
=√2×49×2×9=42m/s
जहां u=0,t=0
गति के समीकरण से h=ut1+12gt21
90=0×t1+12×9.8×t21
अथवा t1=√2×909.8=307=4.28s
जब u=42m/s,t=4.28s
फर्श से टकराने पर गेंद की चाल 10% कम हो जाती है।
∴ अतः प्रथम टक्कर के बाद गेंद का वेग
(v2)=−v−v10
( ∵ प्रत्येक टक्कर के बाद गेंद की चाल 1/10 कम हो जाती है)
=9v10
=910×42=37.8m/s
यदि गेंद फर्श से टकराकर h ऊंचाई तक ऊपर उठती है तो पुनः
गति के समीकरण से
(0)2+(37.8)2−2×9.8×h’
अथवा h’=37.8×37.82×9.8=72.9m
लगा समय t2=√2h’g
=√2×72.99.8=3.857
जब u=37.8m/s,t=3.857s
कुल समय =4.28+3.857=8.137
गेंद को नीच फर्श तक गिरने में पुनः 3.857s समय लगेगा (ऊपर जाने में लगा समय = नीचे आने में लगा समय) जहां फर्श से टकराने से पूर्व उसका वेग 37.8m/s होगा।
फर्श से टकराने पर गेंद का वेग =37.8=37.810=34.02m/s
ऊपर की ओर गति से पहले लगा समय =4.28+3.857+3.857
=11.994s=12s
अतः गेंद t=0s से t=12s के बीच फर्श से टकराकर केवल एक बार ऊपर उठती है तथा इसके लिए चाल समय ग्राफ चित्र में प्रदर्शित किया गया है।
Topper's Solved these Questions
- सरल रेखा में गति Book:BALAJI PUBLICATIONChapter:सरल रेखा में गति Exercise:अतिरिक्त अभ्यास
Explore 5 Videos
- सरल रेखा में गति Book:BALAJI PUBLICATIONChapter:सरल रेखा में गति Exercise:बहुविकल्पीय प्रश्न
Explore 20 Videos
- समतापी तथा रुद्धोष्म ऊष्मागतिक प्रक्रम Book:BALAJI PUBLICATIONChapter:समतापी तथा रुद्धोष्म ऊष्मागतिक प्रक्रम Exercise:बहुविकल्पीय प्रश्न
Explore 35 Videos
Similar Questions
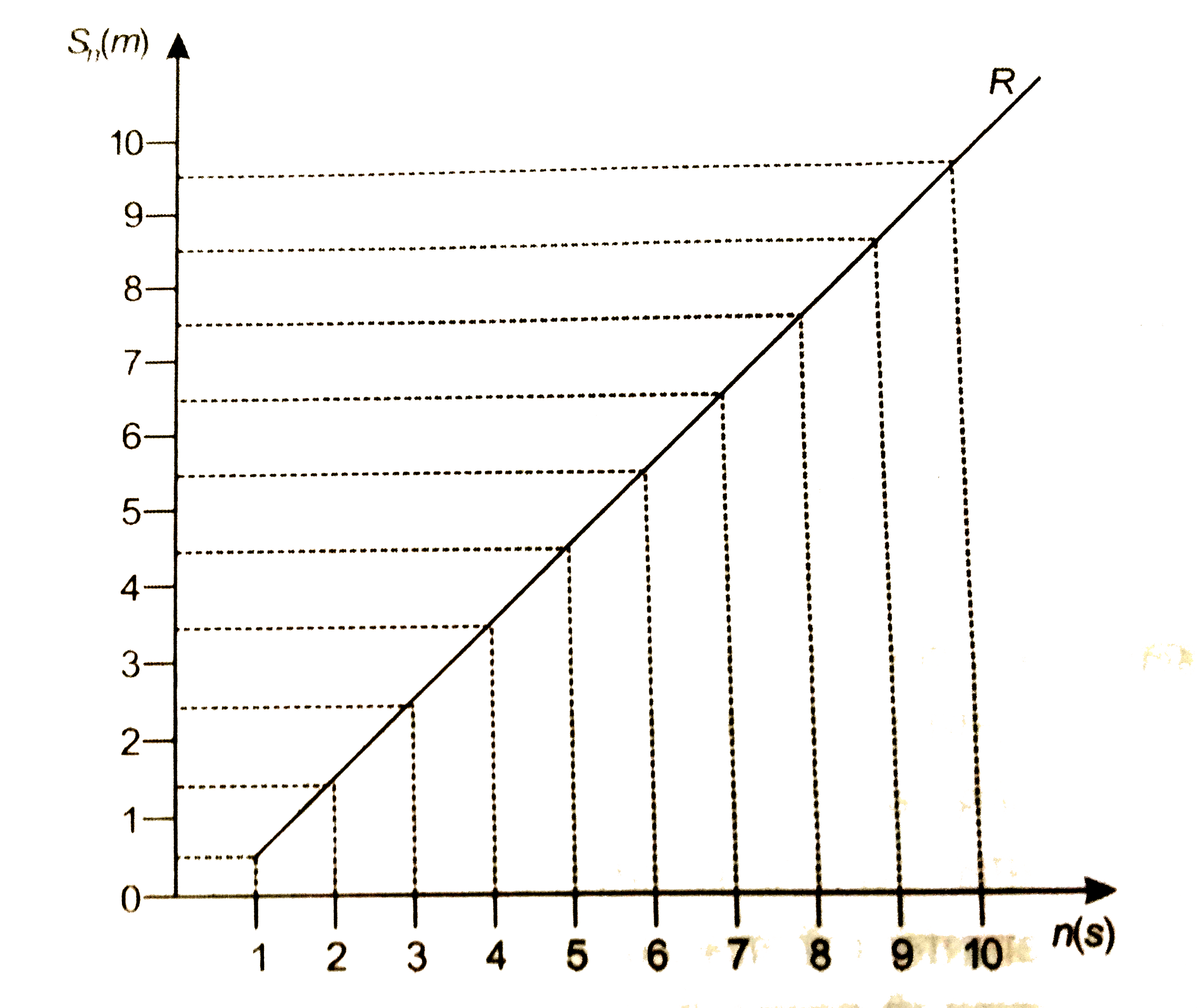
कोई तीन पहिये वाला स्कूटर अपनी विरामावस्था से गति प्रारम्भ करता है । फिर 10s तक किसी सीधी सड़क पर 1m/s2 के एकसमान त्वरण चलता है इनके बाद वह एकसमान वेग से चलता है। स्कूटर द्वारा n वें सेकण्ड (n=1,2,3,………..) में तय की गई को n के सापेक्ष आलेखित कीजिए। आप क्या आशा करते हैं। कि त्वरित गति के दौरान यह ग्राफ कोई सरल रेखा या कोई परवलय होगा?
View Solutionकिसी गतिमान कण के लिए |विस्थापन| का दूरी से अनुपात होता है
View Solutionसमतापीय प्रक्रम में क्या स्थिर रहता है?
View Solutionलोहे की 0.10 किग्रा की एक गेंद 10 मीटर की ऊँचाई से गिराई जाती है तथा पृथ्वी से टकराकर पुनः 1 मीटर की ऊँचाई तक उछल जाती है मान लीजिए कि गेंद कि यान्त्रिक ऊर्जा का क्षय हुआ अंश पूर्णतः गेंद में ही रह जाता है । गेंद है । गेंद के पदार्थ की विशिष्ट ऊष्मा 0.12 कैलोरी /(ग्राम -°C) है । (i) क्या गेंद को ऊष्मा दी गई ?(ii) क्या गेंद पर कार्य किया गया ? यदि हाँ तो कितना ? (iii) गेंद की आन्तरिक ऊर्जा में क्या परिवर्तन हुआ ? (iv) टकराने पर गेंद के ताप में कितनी वृद्धि हुई ?(g=10 न्यूटन /किग्रा , 4.2J = 1 कैलोरी )
View Solutionएक 5 मीटर का लड़का 2 मीटर त्रिज्या के क्षैतिज व्रत में एक प्रथर को डोरी से बांधकर, एकसमान्य चाल से घुमा रहा है व्रत की स्पर्श रेखा के अनुदिश चलते हुवे पृथ्वी पर 10 मीटर की क्षितिज दुरी पर गिरता है वृतीय गति में पत्थर पर कार्यरत अभिक्रिया त्वरण का मान ज्ञात कीजिय ( g = 10 मीटर/सेकण्ड2)|
View Solutionएक 13 मीटर लम्बी सीढ़ी दीवार के सहारे झुकी हुई है। सीढ़ी के पाद को 1.5 मी./से. की दर से जमीन के सारे दीवार से दूर खींचा जाता है। सीढ़ी तथा जमीन के मध्य का कोण किस गति से परिवर्तित हो रहा है जबकि सीढ़ का पावि दीवार से 12 मीटर दूर हो ।
View Solutionएक थैले में 10 गेंदे है जिनमे से प्रत्येक पर से तक के अंको में से अंक लिखा है। यदि थैले से 4 गेंदे उत्तरोत्तर पुनः वापस रखते हुए निकाली जाती है , तो इसी क्या प्रायिकता है कि उनमे से किसी गेंद अंक 0 नहीं लिखा हो ?
View Solutionजब 'r त्रिज्या का एक हवा का बुलबुला किसी झील की तली से सतह तक उठता है तो उसकी त्रिज्या 5r/4 हो जाती है (वायुमण्डलीय दाब जल स्तम्भ की 10 मीटर की ऊंचाई के बराबर है)। यदि ताप नियत है तथा पृष्ठ तनाव को उपेक्षणीय माना गया है, तो झील की गहराई है
View Solutionग्राफ की सहायता से गति के समीकरणों को व्युत्पन्न करना
View Solutionएक थैले में 3 सफेद और 5 काली गेंदें हैं। थैले के अंदर से बिना देखे एक गेंद निकाली जाती है।
(a) एक सफेद गेंद प्राप्त करने की प्रायिकता क्या है?
(b) एक काली गेंद प्राप्त करने की प्रायिकता क्या है?
View SolutionA man goes to a place on car at speed of 160 km/h and comes back at lower speed. If the average speed is 64 km/h in total, them the return speed (in km/h) is:
एक व्यक्ति कार से किसी स्थान को 160 किमी/घंटा की चाल से जाता है तथा कम चाल से वापस आता है | यदि कुल मिलाकर औसत चाल 64 किमी/घंटा है, तो वापसी की चाल (किमी/घंटा में ) है
View Solution4 किमी /घण्टा की चाल से अपने घर से चलकर अमित अपने स्कूल में निर्धारित समय से 10 मिनट पहले पहुंच जाता है। यह वि 3 किमी/घण्टा की चाल से चले, तो निश्चित समय से 10 मिनट देर से पहुंचता है। उसके घर तथा स्कूल के बीच की दूरी है
View SolutionGautam goes to office at a speed of 12 kmph and returns home at 10 kmph. His average speed is गौतम 12 किमी०/घंटा की चाल से कार्यालय जाता है और 10 किमी०/घंटा की चाल से वापस आता है। उसकी औसत चाल बताइए?
View Solutionएक गैस में N_2 अणुओं की वर्ग माध्य मूल चाल u है। यदि तापमान दोगुना हो जाता है और नाइट्रोजन के अणुओं का वियोजन नाइट्रोजन परमाणुओं में हो जाता हैं, तो वर्ग माध्य मूल चाल कितनी होगी?
View Solutionजब एल्कोहॉल की वाष्प को गर्म तांबे के ऊपर से गुजारा जाता है, तो एल्कोहॉल शीघ्रता से एल्कीन में रूपांतरित हो जाती है, एल्कोहॉल है:
View Solutionजल के साथ मिश्रित करने पर SO2 कौन से अम्ल में परिवर्तित हो जाता है?
View Solution
