Surface mass density of disc of mass m and radius R is α−Kr2. Then its moment of inertia w.r.t. axis of rotation passing through center and perpendicular to the plane of disc is :
1=32nR2
1=43nR2
1−25nR2
1−23nR2
The correct Answer is:D
Step by step video, text & image solution for Surface mass density of disc of mass m and radius R is alpha-Kr^(2). Then its moment of inertia w.r.t. axis of rotation passing through center and perpendicular to the plane of disc is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023টপার এই প্রশ্নগুলো সমাধান করেছে
সম্পর্কিত প্রশ্ন
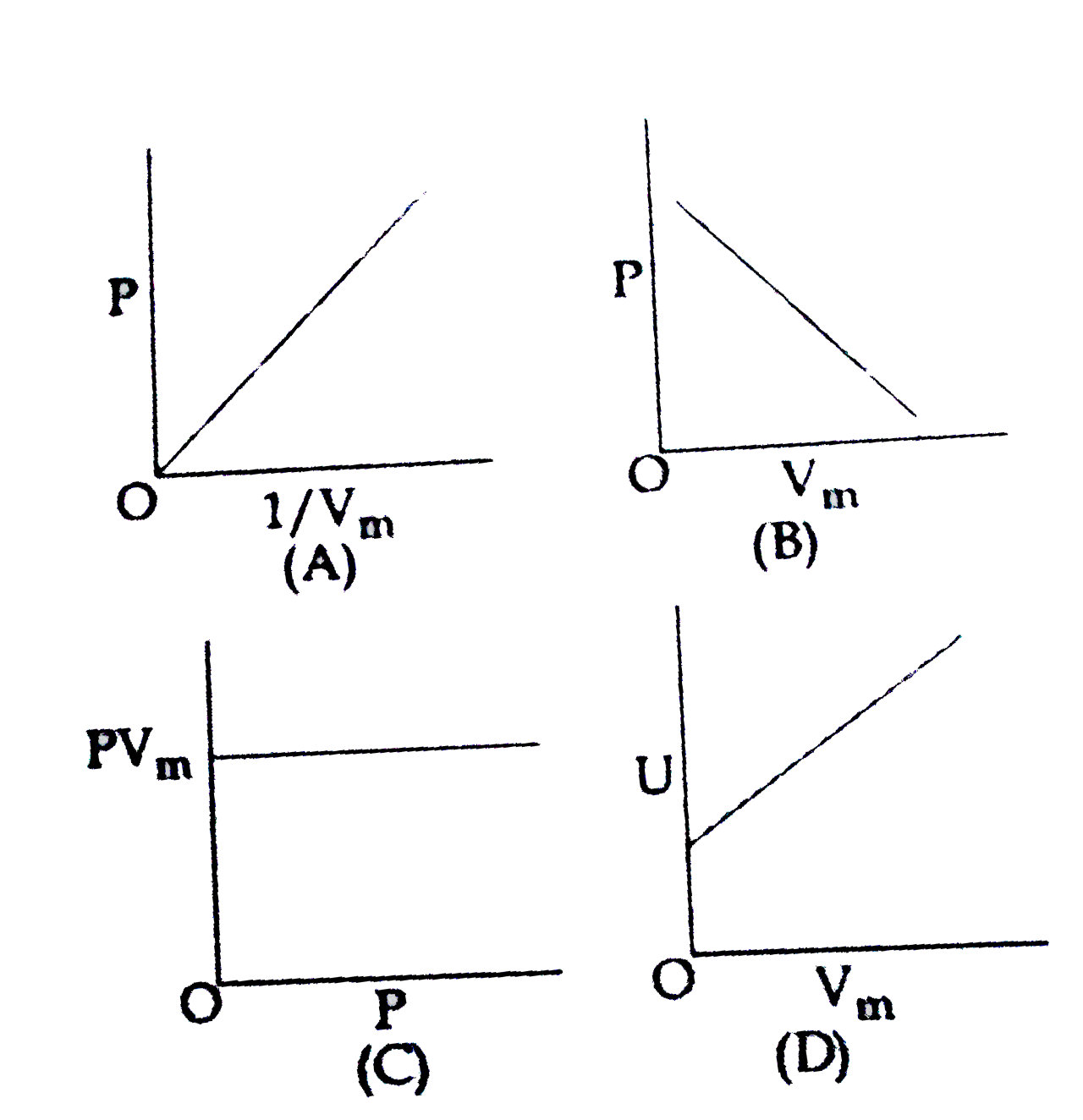
The combination of plots which does not represent isothermal expansion of an ideal gas is :
View SolutionFor the equation of wave y=0.05sin(2x−4t), find velocity of wave.
View SolutionFundamental frequency of two identical strings x and y are 450Hz and 300Hz resp. then find the ratio of tension in string x and y will be
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionThe moment of inertia of a circular disc of mass m and radius r about an perpendicular axis passing through its centre is
View SolutionFrom a circular disc of radius R and 9M , a small disc of mass M and radius R3 is removed concentrically .The moment of inertia of the remaining disc about and axis perpendicular to the plane of the disc and passing through its centre is
View SolutionForm a circular disc of radius R and mass 9M , a small disc of mass M and radius R/3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the the plane of the disc and passing its centre is :-
View SolutionFind the radius of gyration of a disc of mass M and radius R rotating about an axis passing through the center of mass and perpendicular to the plane of the disc.
View Solution1kg द्रव्यमान तथा 2m त्रिज्या की वृत्तीय चकती के तल के लम्बवत्, द्रव्यमान केन्द्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण 2kgm2 है। चकती के सतह से गुजरने वाले अक्ष के समानान्तर जड़त्व आघूर्ण होगा (दिये गये चित्रानुसार)
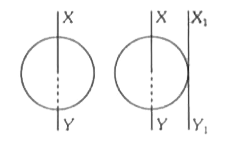
View SolutionSurface mass density of disc of mass m and radius R is Kr^(2) . Then its moment of inertia w.r.t. axis of rotation passing through center and perpendicular to the plane of disc is :
View SolutionFrom a circular disc of radius R and mass 9 M , a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionR त्रिज्या और 9M द्रव्यमान वाली एक चकती से R/3 त्रिज्या तथा M द्रव्यमान वाली एक संकेन्द्रीय छोटी चकती निकाली जाती है । शेष बची चकती का उसके तल के लंबवत तथा केंद्र से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण लेगा -
View Solution
