मूलबिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की संख्या होगी ?
निर्देश -
यदि रेखाएँ 3x−4y−7=0 तथा 2x−3y−5=0 उस वृत्त के दो व्यास है, जिसका क्षेत्रफल 49π वर्ग इकाई है, तब
0
1
2
इनमे से कोई नहीं
The correct Answer is:A
∵ मूलबिन्दु वृत्त x2+y2=a2 के केन्द्र के निर्देशांक है, इसलिए इस वृत्त पर कोई भी स्पर्श रेखा खींची नहीं जा सकती है, अतः स्पर्श रेखाओं की संख्या शून्य होगी।
दिए गए व्यासो के समीकरण निम्न है
3x−4y−7=0 ….(i)
2x−3y−5=0 ....(ii)
समी (i) व (ii) को हल करने पर,
x = 1 तथा y = - 1
∴ वृत्त का केन्द्र (1, -1) है
मान लीजिए वृत्त की त्रिज्या r है, तब
πr2=49π
implies r = 7 इकाई
∴ वृत्त का समीकरण (x−1)2+(y+1)2=49
⇒x2+y2−2x+2y−47=0
तथा वृत्त के केन्द्र से बिन्दु (5, 2) को मिलाने वाले रेखाखण्ड का समीकरण
(y−2)=−1−21−5(x−5)
⇒(y−2)=−3−4(x−5)
⇒3x−4y−7=0
टॉपर्स ने हल किए ये सवाल
समान प्रश्न
उस वृत्त का क्षेत्रफल (वर्ग इकाई में), जिसका केन्द्र (1, 2) है तथा जो बिन्दु (4, 6) से होकर जाता है, है
View Solution9+2√14 का वर्गमूल होगा
View Solutionदीर्घवृत्त 5x2+9y2=45 के नाभिलम्ब की लम्बाई है
View Solutionरेखा तथा वृत्त के स्पर्श बिंदु के निर्देशांक ……………. है ।
View Solutionबिंदु (−2,1) से वृत्त 2x2+2y2−3x−4y−1=0 पर खींची गयी स्पर्श रेखा की लम्बाई ………….. इकाई है ।
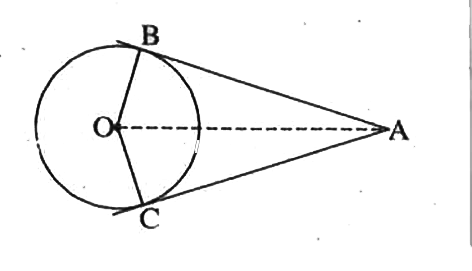
View Solutionदी गई आकृति में AB तथा AC वृत्त की स्पर्श रेखाएं है ,O वृत्त का केंद्र है ,यदि ∠CAB=60∘ तो ∠BOC है -
View Solutionदी गई आकृति AT वृत्त की स्पर्श रेखा है। यदि m∠ABC=50∘ तथा AC=BC तो ∠BAT है -

View Solutionदो वृत्त जिसकी त्रिज्याएँ 3 सेमी एवं 4 सेमी है। जिनके केन्द्रो के बाध्य की दूरी 8 सेमी है। दोनों वृतो पर उभयनिष्ठ स्पर्श रेखाएं कीतिनि खींची जा सकती है ?तथा दो उभयनिष्ठ अनुस्पर्श रेखाओ की रचना कीजि।
View Solutionवृत्त के बाहर स्थित बिंदु से खींची गई स्पर्श रेखाओं की संख्या हो सकती है:
View Solutionमाना PQ और RS,r त्रिज्या के वृत्त के व्यास के सिरों पर खींची गई स्पर्शियाँ है। यदि PS और RQ परिधि पर स्थिति बिन्दु X पर प्रतिच्छेद करते है तो 2r बराबर है-
View Solutionवृत्त x2+y2=4 के बिंदु (√3,1) पर खींची गई स्पर्श रेखा और अभिलम्ब तथा X-अक्ष एक त्रिभुज बनाते है । इस त्रिभुज का (वर्ग इकाइयो में) क्षेत्रफल है
View Solutionसरल रेखा x+2y=1 निर्देशांक अक्षों को A तथा B पर काटती है। मूलबिंदु , A तथा B से होकर जाने वाला वृत्त खींचा गया है , तो मूलबिंदु पर वृत्त की स्पर्श रेखा की A तथा B से लम्बवत दूरियों का योग है
View Solutionयदि बिन्दु (1, 2) से वृत्त x2+y2−2x−4y+λ=0 पर असंख्य स्पर्श रेखाएं खींची जा सकती हों, तो λ का मान है।
View Solutionवृत्त x2+y2=169 के बिन्दुओं (5, 12) तथा (12,-5) पर खींची गई स्पर्श रेखाओं के बीच का कोण है
View Solutionपरवलय y2=4a(x−a) पर मूलबिन्दु से खींची गयी स्पर्श रेखाओं के बीच का कोण है
View Solutionमाना एक वृत्त है जिसका केन्द्र परवलय y2=2px की नाभि पर है, तथा यह वृत्त परवलय की नियता को स्पर्श करता है, तो वृत्त व परवलय का प्रतिच्छेद बिंदू है
View Solution
