The friction coefficient bettween an athelete's shoes nd the ground is 0.90. Supose a superman wears these shoes and rces for 50 m. There is no upper limit n his capacity of running at high speeds. A. Find the minimum time tht he will have to take in completing the 50 m starting from rest. b. Suppose he takes exactly this minimum time to complete the 50 m, what minimum time will he take to stop?
To solve the problem step by step, we will break it down into two parts:
Part A: Finding the Minimum Time to Complete 50 m
1. Identify the given data:
- Coefficient of friction (μ) = 0.90
- Distance (s) = 50 m
- Initial velocity (u) = 0 m/s (starting from rest)
2. Calculate the maximum acceleration (a):
The maximum frictional force provides the maximum acceleration. The formula for maximum frictional force (f_max) is:
fmax=μ⋅N
where N is the normal force. For a horizontal surface, N=mg (mass times gravitational acceleration).
Thus,
fmax=μ⋅mg
Using Newton's second law, f=ma, we have:
ma=μmg
This simplifies to:
a=μg
Substituting the values:
a=0.90⋅10m/s2=9m/s2
3. Use the kinematic equation to find time (t):
The equation we will use is:
s=ut+12at2
Since u=0:
50=0+12⋅9⋅t2
Simplifying gives:
50=92t2
Rearranging:
t2=1009
Taking the square root:
t=√1009=103≈3.33s
Part B: Finding the Minimum Time to Stop
1. Determine the initial velocity (u) when he finishes running:
The final velocity (v) after running 50 m can be calculated using:
v=u+at
Since u=0:
v=0+9⋅103=30m/s
2. Calculate the time to stop:
When stopping, the final velocity (v) is 0, and the initial velocity (u) is 30 m/s. The acceleration (a) will be negative (deceleration) and equal to −9m/s2.
Using the formula:
v=u+at
Rearranging gives:
0=30−9t
Solving for t:
9t=30⟹t=309=103≈3.33s
Final Answers:
- Part A: The minimum time to complete 50 m is approximately 3.33 seconds.
- Part B: The minimum time to stop is also approximately 3.33 seconds.
- Coefficient of friction (μ) = 0.90
- Distance (s) = 50 m
- Initial velocity (u) = 0 m/s (starting from rest)
The maximum frictional force provides the maximum acceleration. The formula for maximum frictional force (f_max) is:
fmax=μ⋅N
where N is the normal force. For a horizontal surface, N=mg (mass times gravitational acceleration).
Thus,
fmax=μ⋅mg
Using Newton's second law, f=ma, we have:
ma=μmg
This simplifies to:
a=μg
Substituting the values:
a=0.90⋅10m/s2=9m/s2
The equation we will use is:
s=ut+12at2
Since u=0:
50=0+12⋅9⋅t2
Simplifying gives:
50=92t2
Rearranging:
t2=1009
Taking the square root:
t=√1009=103≈3.33s
The final velocity (v) after running 50 m can be calculated using:
v=u+at
Since u=0:
v=0+9⋅103=30m/s
When stopping, the final velocity (v) is 0, and the initial velocity (u) is 30 m/s. The acceleration (a) will be negative (deceleration) and equal to −9m/s2.
Using the formula:
v=u+at
Rearranging gives:
0=30−9t
Solving for t:
9t=30⟹t=309=103≈3.33s
- Part A: The minimum time to complete 50 m is approximately 3.33 seconds.
- Part B: The minimum time to stop is also approximately 3.33 seconds.
Topper's Solved these Questions
Similar Questions
Knowledge Check
To complete a work, A takes 50% more time than B. If together they take 18 days to complete the work, how much time shall B take to do it ?
A30 daysB35 daysC40 daysD45 daysTo complete a wall, X takes 20% more time than Y. If together they complete the wall in 30 days, how much time (in days) will Y alone take to complete it?
A30 daysB35 daysC40 daysD45 daysThe complete a work, A takes 50 % more time than B. If together they takes 18 days to do complete the work, then B takes the time to do the work in :
A30 daysB35 dyasC40 daysD45 days
On a horizontal rought rood , value of coefficient of friction μ=0.4.Find the minimum time in which a distance of 400m can be covered. The car start from rest and finally comes to rest.
View SolutionDivede a plane 10m long and 5m high into three parts so that a body starting from rest takes equal times to slide down these. Also find the time taken then.
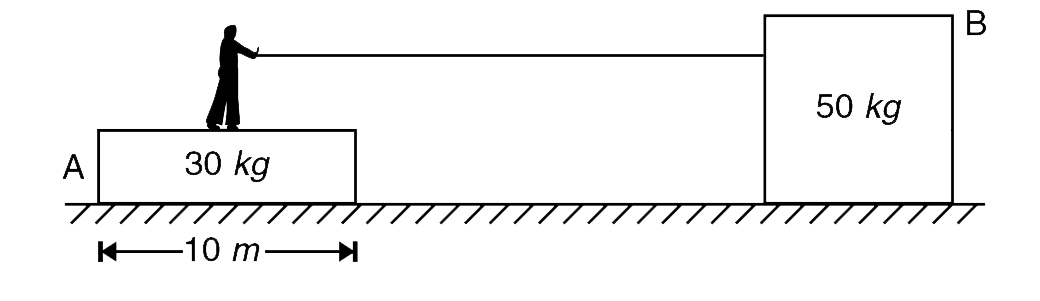
View SolutionA 50 kg man is standing at the centre of a 30 kg platform A. Length of the platform is 10 m and coefficient of friction between the platform and the horizontal ground is 0.2. Man is holding one end of a light rope which is connected to a 50 kg box B. The coefficient of friction between the box and the ground is 0.5. The man pulls the rope so as to slowly move the box and ensuring that he himself does not move relative to the ground. If the shoes of the man does not slip on the platform, calculate how much time it will take for the man to fall off the platform. Assume that rope remains horizontal, and coefficient of friction between shoes and the platform is 0.6.
View SolutionThe coefficient of friction between the tyres and road is 0.4. The minimum distance covered before attaining a speed of 8 ms−1 starting from rest is nearly (take, g=10 ms−2)
View SolutionThe coefficient of friction between the tyres and road is 0.4. The minimum distance covered before attaining a speed of 8ms−1 starting from rest is nearly ( take g=10ms−2)
View Solution
