The two blocks in an Atwood machine have masses 2.0 kg and 3.0 kg. Find the work done by gravity during the fourth second after the system is released from rest.
To solve the problem of finding the work done by gravity during the fourth second after the system is released from rest in an Atwood machine with masses 2.0 kg and 3.0 kg, we can follow these steps:
Step 1: Identify the masses and the gravitational force
We have two masses:
- m1=2.0kg (the lighter mass)
- m2=3.0kg (the heavier mass)
The gravitational force acting on each mass is given by:
- For m1: Fg1=m1⋅g=2.0kg⋅10m/s2=20N
- For m2: Fg2=m2⋅g=3.0kg⋅10m/s2=30N
Step 2: Determine the acceleration of the system
Using Newton's second law, we can set up the equations for both masses.
For the 3 kg mass (going down):
m2g−T=m2a⇒30−T=3a(1)
For the 2 kg mass (going up):
T−m1g=m1a⇒T−20=2a(2)
Adding equations (1) and (2):
30−20=3a+2a⇒10=5a⇒a=2m/s2
Step 3: Calculate the distance traveled during the fourth second
The distance traveled by the masses during the nth second can be calculated using the formula:
sn=u+a2(2n−1)
Since the system starts from rest, u=0:
s4=0+22(2⋅4−1)=1⋅(8−1)=7m
Step 4: Calculate the work done by gravity
The work done by gravity on each mass can be calculated as follows:
For the 3 kg mass (going down):
Wg2=m2⋅g⋅h=3⋅10⋅7=210J
For the 2 kg mass (going up):
Wg1=−(m1⋅g⋅h)=−(2⋅10⋅7)=−140J
Step 5: Calculate the net work done by gravity
The net work done by gravity on the system during the fourth second is:
Wnet=Wg2+Wg1=210J−140J=70J
Final Answer
The work done by gravity during the fourth second after the system is released from rest is 70 Joules.
---
We have two masses:
- m1=2.0kg (the lighter mass)
- m2=3.0kg (the heavier mass)
- For m1: Fg1=m1⋅g=2.0kg⋅10m/s2=20N
- For m2: Fg2=m2⋅g=3.0kg⋅10m/s2=30N
Using Newton's second law, we can set up the equations for both masses.
m2g−T=m2a⇒30−T=3a(1)
T−m1g=m1a⇒T−20=2a(2)
30−20=3a+2a⇒10=5a⇒a=2m/s2
The distance traveled by the masses during the nth second can be calculated using the formula:
sn=u+a2(2n−1)
Since the system starts from rest, u=0:
s4=0+22(2⋅4−1)=1⋅(8−1)=7m
The work done by gravity on each mass can be calculated as follows:
Wg2=m2⋅g⋅h=3⋅10⋅7=210J
Wg1=−(m1⋅g⋅h)=−(2⋅10⋅7)=−140J
The net work done by gravity on the system during the fourth second is:
Wnet=Wg2+Wg1=210J−140J=70J
The work done by gravity during the fourth second after the system is released from rest is 70 Joules.
Topper's Solved these Questions
Similar Questions
Consider two observers moving with respect to each other at a speed v along a straighline. They observe a block of mass m movig a distasnce l on a rough surface. The following quantities will be same as observed by the two observers
View SolutionA wave pulse passing on a string with speed of 40cms−1 in the negative x direction has its maximum at x=0att=0. Where will this maximum be located at t=5s?
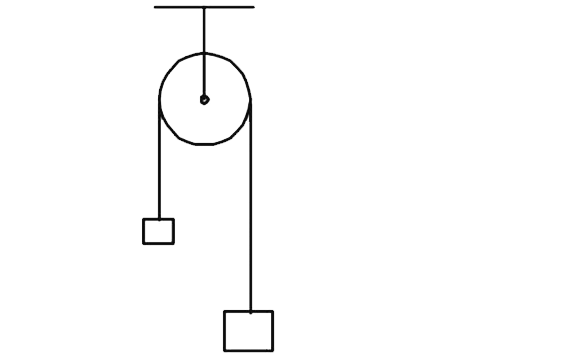
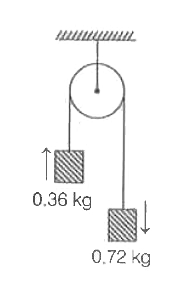
View SolutionA light inextensible string that gas over a smoth fixed polley as shown in the figure connect two blocks of mases it 0.36 kg and 0.72 kg Taking g=10ms−2 , find the work done by the string on the block of mass 0.36 kg doring the first second after the system is refosed from rest ,
View SolutionTwo uneqal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown . If the system is released from rest, find the work done by string on both the blocks in 1 s.
(Take g=10m/s2).
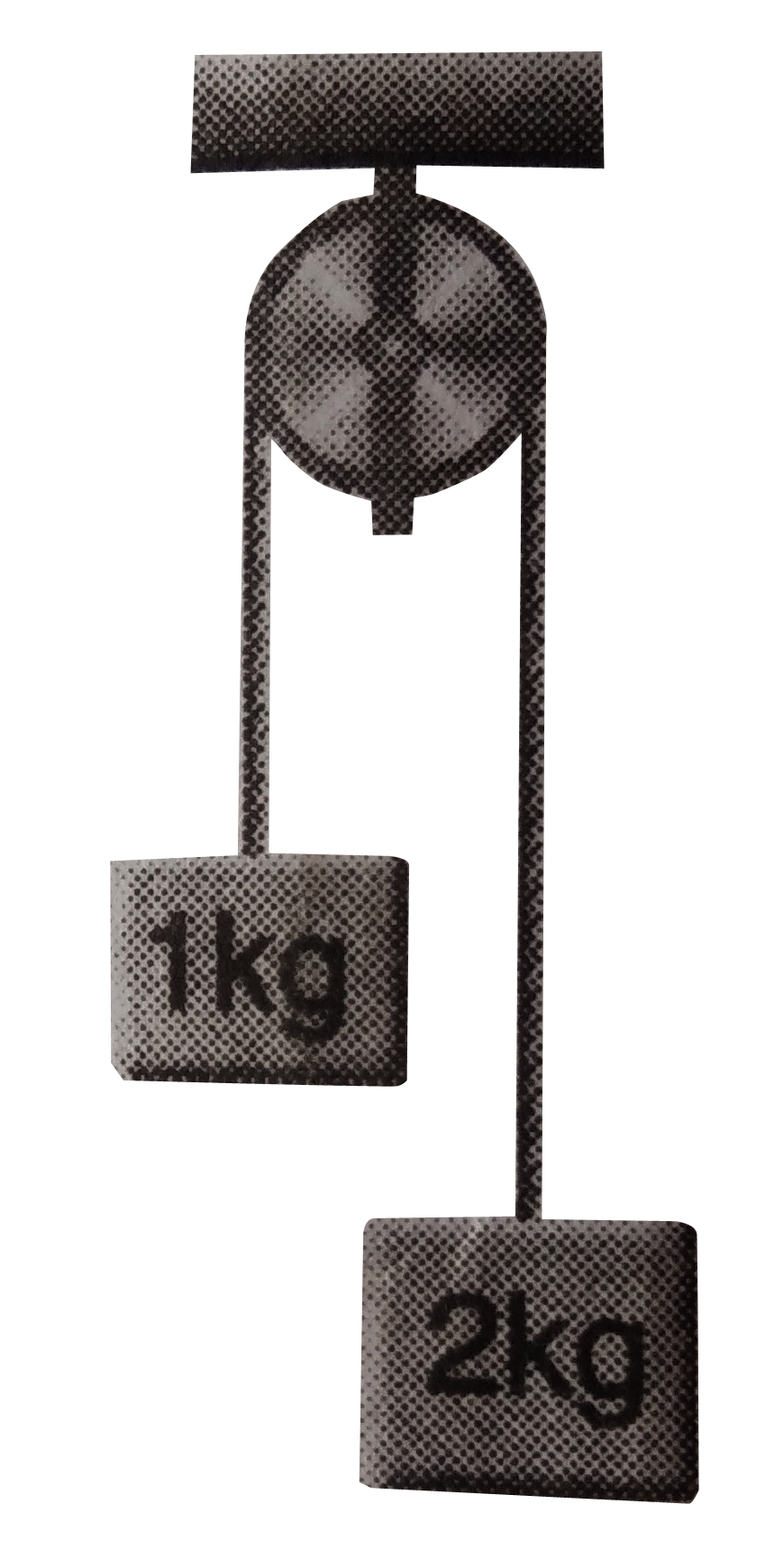
View SolutionIn the pulley-block system shown in figure, strings are light. Pulleys are massless and smooth. System is released from rest. In 0.3 seconds.
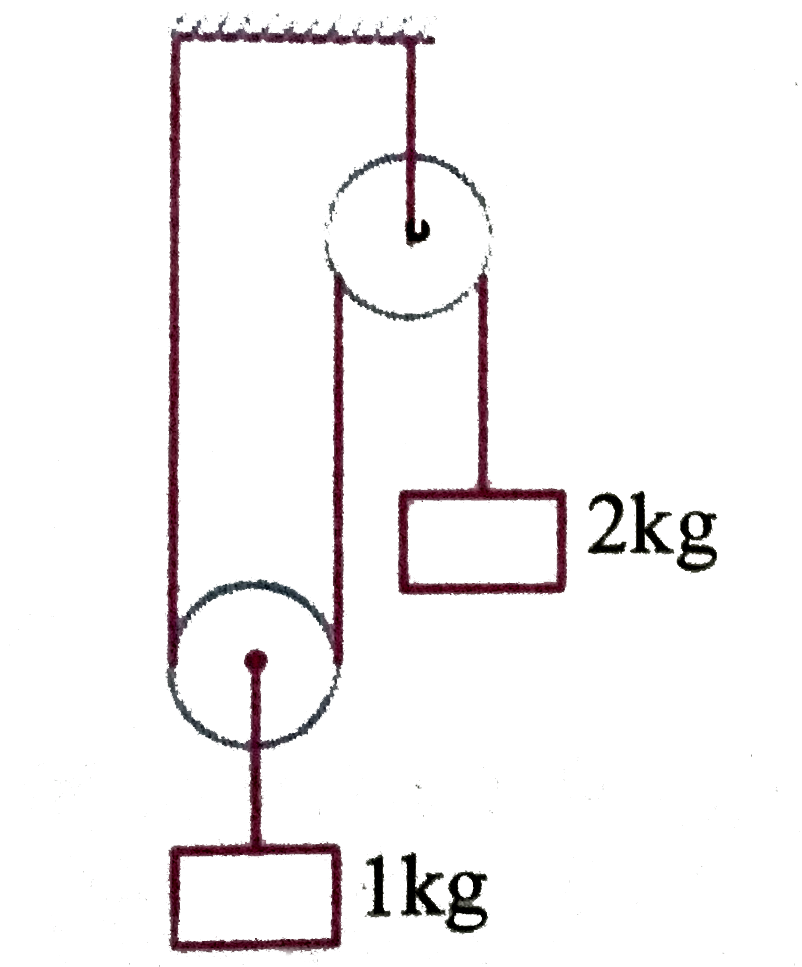 .
.
(a) work done on 2kg block by gravity is 6J
(b) work done one 2kg block by string is −2J
( c) work done on 1kg block by gravity is −1.5J
(d) work done on 1kg block string is 2J.
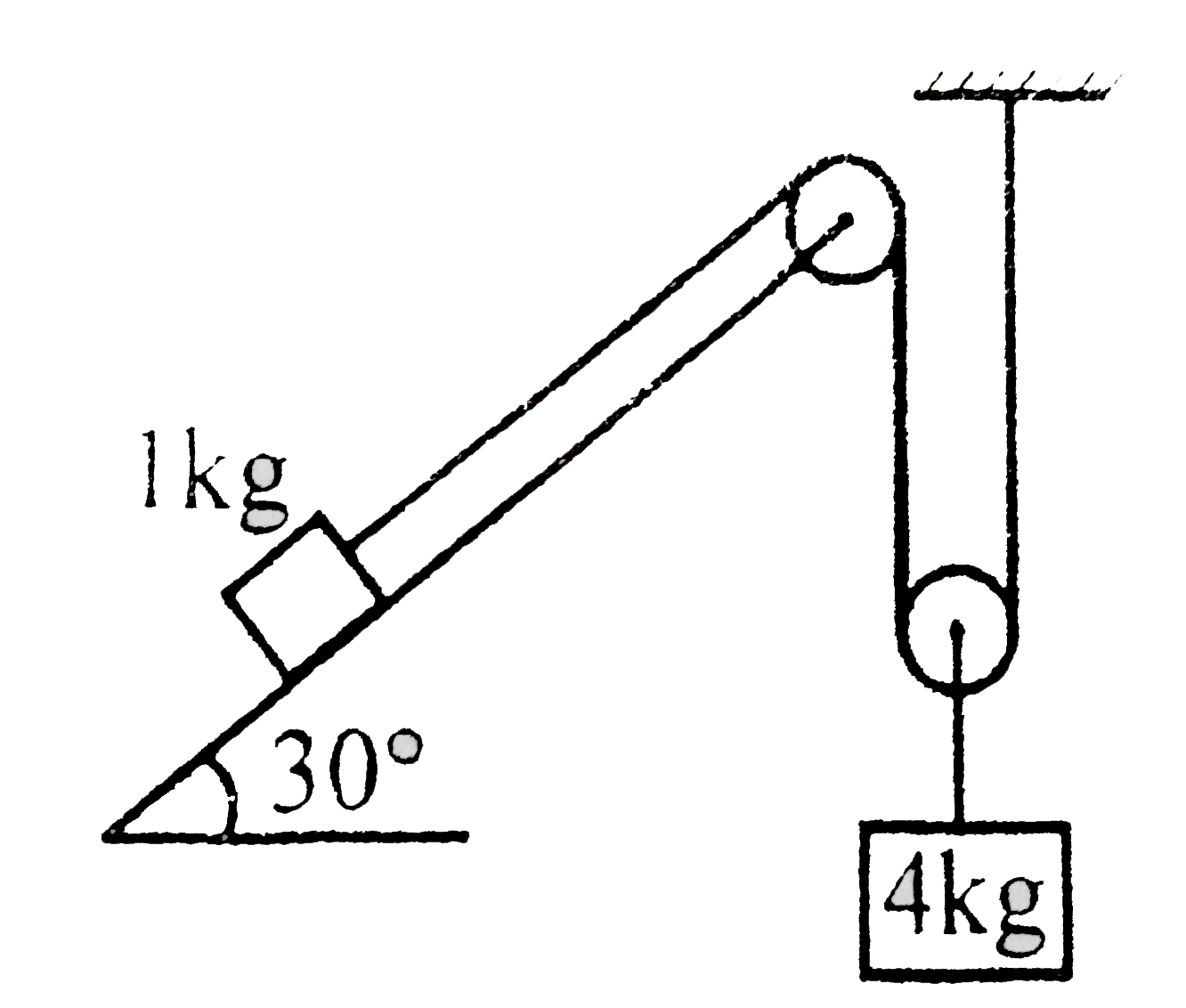
View SolutionFind the work done by tension (in J) on 1 kg block when 4 kg block moves down by 20 cm after the system is released. All surfaces are frictionless
View Solution2.0 किग्रा तथा 1.0 किग्रा के दो पिण्ड 3.0 मीटर दूरी पर स्थित है| निकाय के द्रव्यमान केन्द्र की स्थिति ज्ञात कीजिए|
View Solutionएक एटबुड मशीन में घिरनी पर से जाती डोरी से बंधे गुटको के द्रव्यमान क्रमशः 2.0kg तथा 3.0 kg हैं। विरामावस्था से छोड़ने के बाद चौथे सेकड में गुरुत्वाकर्षण बल द्वारा गुटकों पर किया गया कुल कार्य ज्ञात करे
View SolutionIn the pulley - block system shown in figure, strings are light. Pulleys are massless and smooth. System is released from rest. In 0.3 seconds a) work done on 2 kg blocks by gravity is 6 J b) work done on 2 kg block by string is -2J c) work done on 1 kg block by gravity is -1.5 J d) work done on 1 kg block by string is 2 J
View SolutionIn the arrangement shown in the figure work dione by the string on the block of mass 0.36 kg during the first second after the blocks are released from state of rest is (Ignotre friction and mass of the string )
(acceleration due ot gravity g=10ms−2)
View Solutionस्प्रिंग स्थिरांक 5X103 N/m का एक स्प्रिंग प्रारंभ में बिना खिंचाव वाली स्थिति से 10 सेमी तक खींचा जाता है। फिर, इसे और 10 सेमी और बढ़ाने के लिए आवश्यक कार्य है
View SolutionThe blocks A and B shown in the figure have masses M_A = 5 kg and M_B = 4 kg . The system is released from rest. The speed of B after A has travelled a distance 1 m along the incline is
View SolutionThe heavier block in an atwood machine has a mass twice that of the lighter one. The tension in the string is 16.0 N when the system is set into motion. Find the decrease in the gravitational potential energy during the first second after the system is released from rest.
View SolutionThe system shown in figure is released from rest. String is massless, and pulley is smooth. Find work done by gravity on 4kg block and workdone by the string on 1 kg block in 2 seconds?
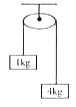
View SolutionThe system shown in the figure is released from rest. Mass of the block on the table is 4 kg and mass of the other block is 1 kg. Coefficient of kinetic friction between block and table is 0.12. Find the speed of 1 kg block after it has descended through a distance of 1m.
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown . If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g= 10 m//s^2 ).
View Solution

