A man of maas m is standing on a platform of maas M kept on smooth ice. If the man starts moving on the platform with a speed v relative to the platform with what velcity relative to the ice does the platform recoil?
To solve the problem step by step, we will use the principle of conservation of momentum.
Step 1: Understand the system
We have a man of mass m standing on a platform of mass M on smooth ice. Initially, both the man and the platform are at rest.
Step 2: Define the velocities
- Let v be the velocity of the man relative to the platform.
- Let V be the velocity of the platform relative to the ice.
- The velocity of the man relative to the ice will then be V−v because he moves in the opposite direction to the platform's motion.
Step 3: Apply conservation of momentum
Since there are no external forces acting on the system (the ice is smooth), the total momentum before and after the man starts moving must be conserved.
Initially, the total momentum Pinitial is:
Pinitial=0(since both are at rest)
After the man starts moving, the total momentum Pfinal is:
Pfinal=m(V−v)+M(−V)
Here, m(V−v) is the momentum of the man, and M(−V) is the momentum of the platform (moving in the opposite direction).
Step 4: Set up the equation
Setting the initial momentum equal to the final momentum gives:
0=m(V−v)−MV
Step 5: Rearranging the equation
Rearranging the equation, we get:
m(V−v)=MV
Expanding this gives:
mV−mv=MV
Step 6: Isolate V
Now, we can isolate V:
mV−MV=mv
V(m+M)=mv
V=mvm+M
Conclusion
Thus, the velocity of the platform relative to the ice is:
V=mvm+M
We have a man of mass m standing on a platform of mass M on smooth ice. Initially, both the man and the platform are at rest.
- Let v be the velocity of the man relative to the platform.
- Let V be the velocity of the platform relative to the ice.
- The velocity of the man relative to the ice will then be V−v because he moves in the opposite direction to the platform's motion.
Since there are no external forces acting on the system (the ice is smooth), the total momentum before and after the man starts moving must be conserved.
Pinitial=0(since both are at rest)
Pfinal=m(V−v)+M(−V)
Here, m(V−v) is the momentum of the man, and M(−V) is the momentum of the platform (moving in the opposite direction).
Setting the initial momentum equal to the final momentum gives:
0=m(V−v)−MV
Rearranging the equation, we get:
m(V−v)=MV
Expanding this gives:
mV−mv=MV
Now, we can isolate V:
mV−MV=mv
V(m+M)=mv
V=mvm+M
Thus, the velocity of the platform relative to the ice is:
V=mvm+M
Similar Questions
A boy of mass m is standing on a platform of M kept on smooth floor. If the body starts moving on the platform with a speed v0 relative to the platform , with what velocity to the floor does the platform recoil ?
View SolutionA man of mass m1 is standing on a platform of mass m2 kept on a smooth horizontal surface. The man starts moving on the platform with a velocity vr relative to the platform. Find the recoil velocity of platform.
View Solution
Knowledge Check
A man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is
 A2uBu2CzeroDu4
A2uBu2CzeroDu4
A man of mass m=2kg is standing on a platform of mass M=5kg, then at any instant.
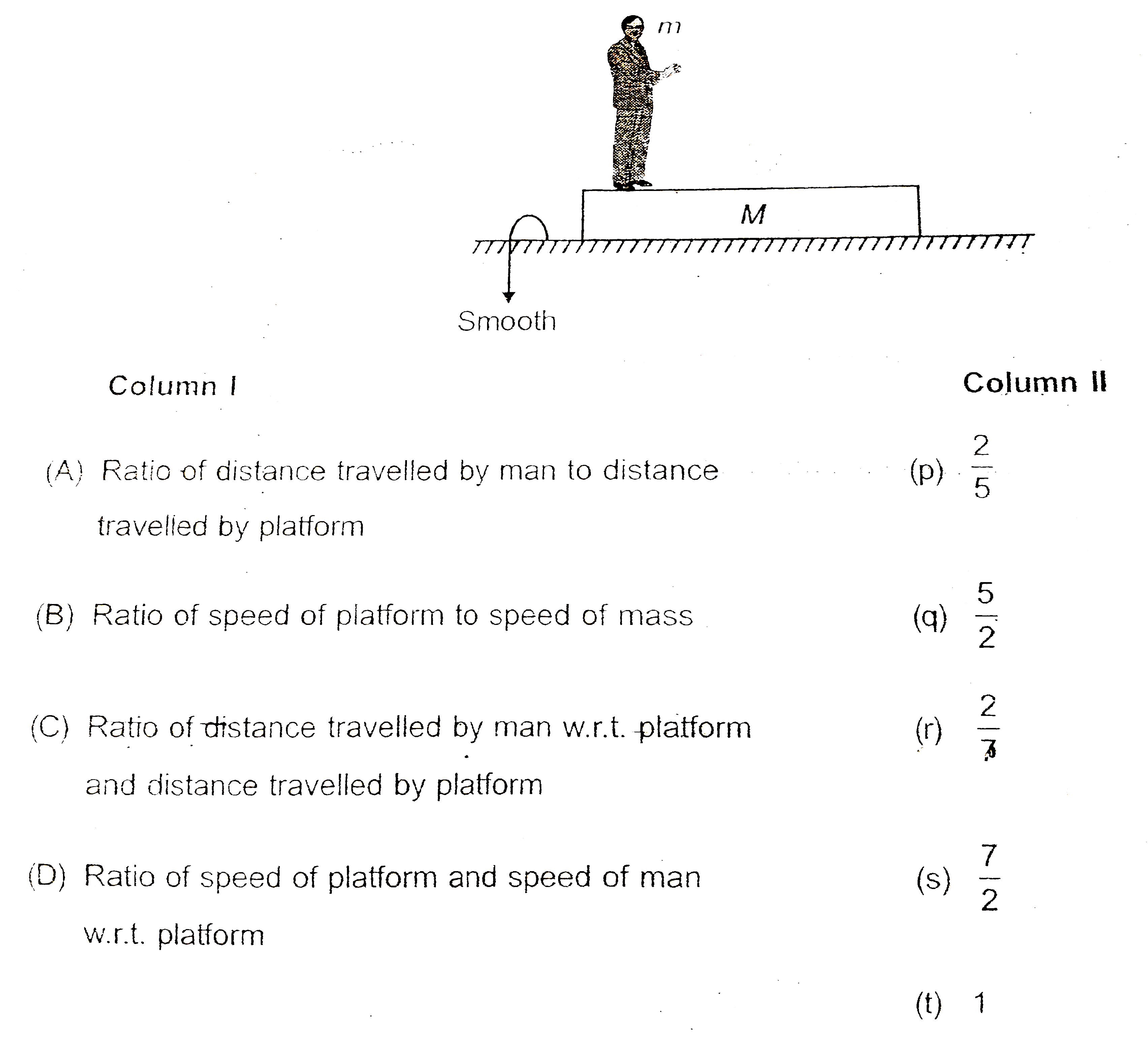
View SolutionA man of mass m1 = 80 kg is standing on a platform of mass m2 = 20 kg that lies on a frictionless horizontal surface. The man starts moving on the platform with a velocity vr = 10 m/s relative to the platform. Find the recoil speed of the platform.
View SolutionA man of mass m1 is standing on a platform of mass m2 kept on a smooth horizontal surface. If the man moves a distance d w.r.t., the platform, find the displacement of the platform w.r.t., ground.
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
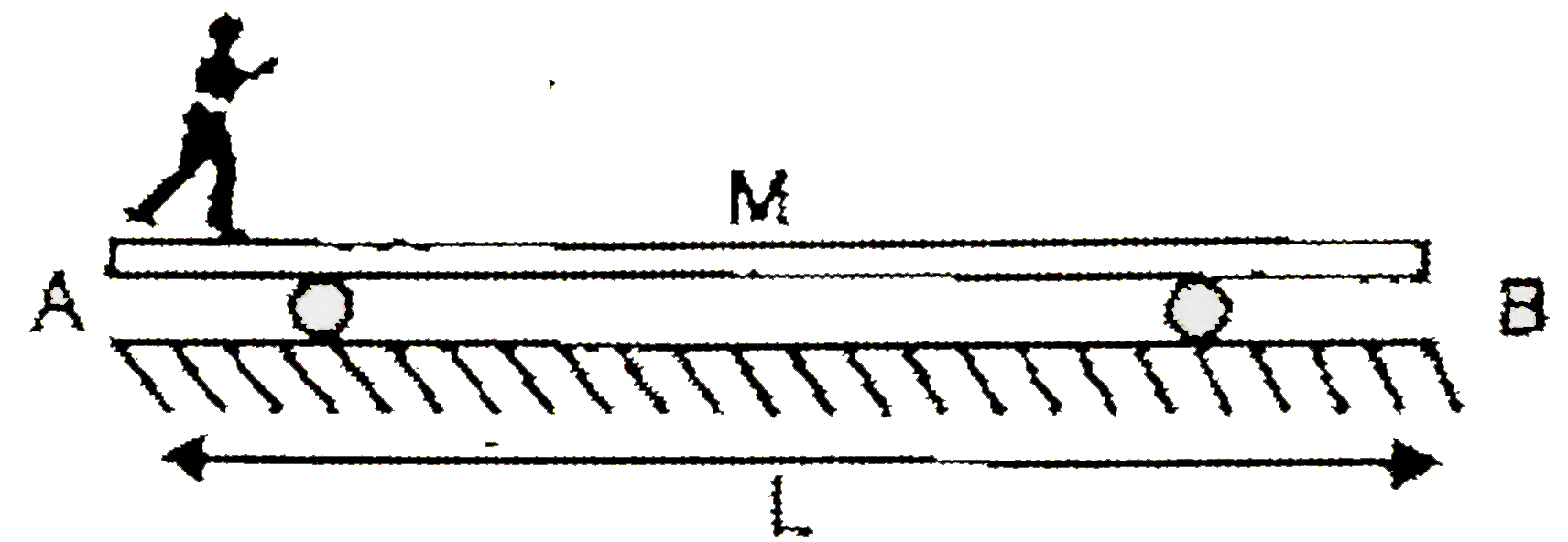
When the man starts moving, then the velocity of the trolley v2 with respect to ground will be:
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
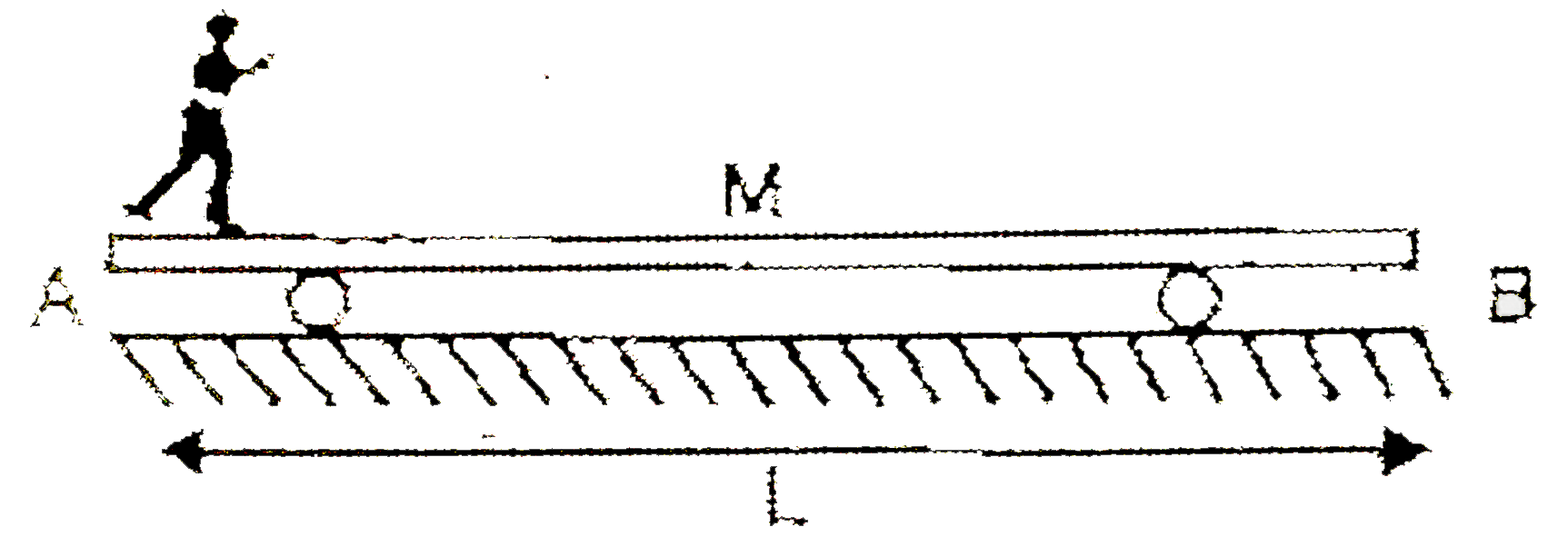
The velocity of the man with respect to ground v1 will be:
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
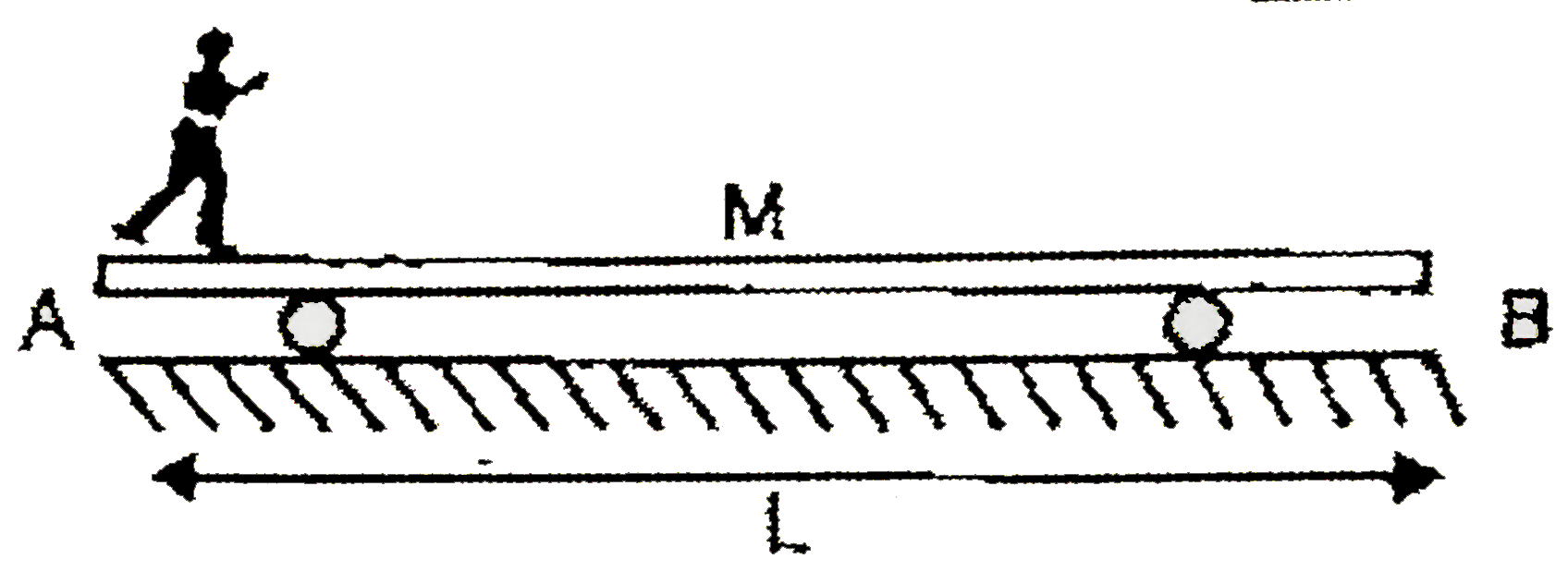
As the man walks on the trolley, the centre of mass of the system (man+ trolley) :
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.

When the man reaches the end B, the distance moves . by the trolley with respect to ground is:
View Solution

