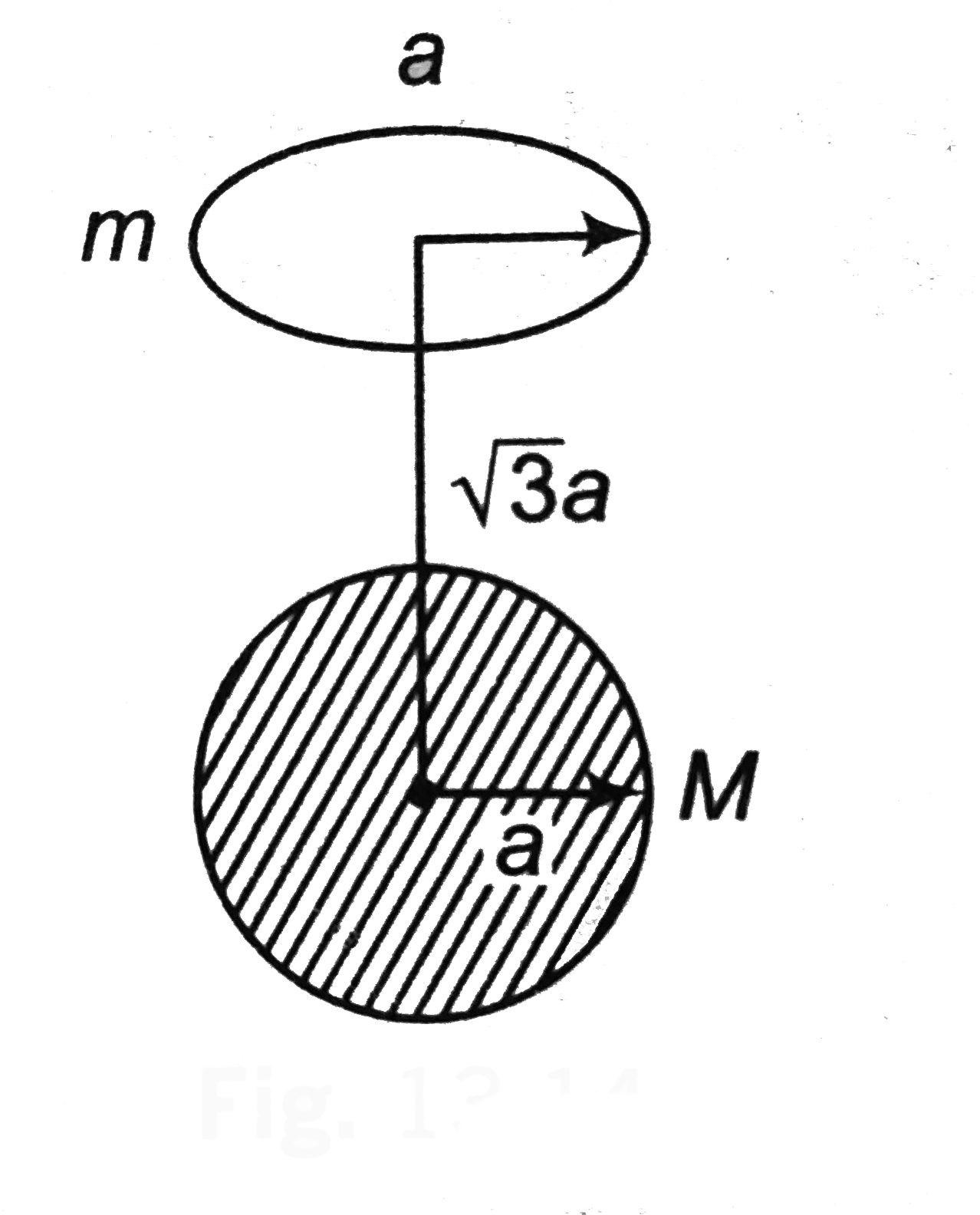
A uniform rig of mas m and radius a is placed directly above a uniform sphre of mass M and of equyal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational foerce exerted by the sphere on the ring.
The gravitatioN/Al field at any on the ring due to the sphere is equal to the field due to a isngle particle of mass M laced at the centre of the sphre.Thus, theforce on the ring due to the sphere is also equla to the force on it by a particle of mas M placed at this point.By Newton's third laaw it is equal to the force on the particle by the rig. Now the gravitatioN/Al field due to the ring at a distance d=√3 a on its axis is
E=Gmd(a2+d2)32=(sqrt3Gm)/(8a^2)<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/HCV_VOL1_C11_S01_018_S01.pngwh=80%sty≤=max-width:280px;background:white;margin-top:12px;margin-bottom:12px;><br>Theforceonaartic≤ofmasssMplacedhereis<br>F=ME<br>=(sqrt3GMm)/(8a^2)
This is also the force due to the sphere on the ring
Topper's Solved these Questions
- GRAVITATIONBook:HC VERMAChapter:GRAVITATIONExercise:Short Answer
Explore 19 Videos
- GRAVITATIONBook:HC VERMAChapter:GRAVITATIONExercise:Objective 1
Explore 17 Videos
- GRAVITATIONBook:HC VERMAChapter:GRAVITATIONExercise:Exercises
Explore 39 Videos
- FRICTIONBook:HC VERMAChapter:FRICTIONExercise:Exercises
Explore 31 Videos
- HEAT AND TEMPERATUREBook:HC VERMAChapter:HEAT AND TEMPERATUREExercise:Exercise
Explore 4 Videos
Similar Questions
A uniform ring of mass 2m and radius a is placed directly above the uniform sphere of mass M and of same radius. The centre of ring is at distance √3a from the centre of sphere. The gravitational force exerted by the sphere on the ring is NGMma2 units. Calculate is the value of N?
View SolutionA uniform ring of mass m is lying at a distance √3 a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
View Solution
Knowledge Check
A uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
AGM2R2B3GM22R3C2GM2√2R2D√3GM2R2A uniform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and of same radius R. The centre of the ring is at a distance of d=√3R from the centre of the sphere. The gravitational attraction between the sphere and the ring is
AGM2R2B3GM2R3C2GM2√2R2D√3GM2R2A uiform ring of mass M and radius R is placed directly above a uniform sphere of mass 8M and same radius R. The centre of the sphere. The gravitational atraction between the sphere and the ring is
A8GM2R2B2GM2√3R2C3GM22R2D√32GM2R2
A particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View SolutionFor a uniform ring of mass M and radius R at its centre
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionInside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
View Solution
