Find the time period of small oscillations of the following system. a. A metre stick suspended through the 20 cm mark. b. A ring of mas m and radius r suspended through a pointon it speriphery. c. A uniform sdquare plate of edge a suspended through a corner. d. A uniform disc of mass m and radius r suspended through a point r2 away from the centre.
The correct Answer is:A, B, C, D
a. M.I. about the pt a=1=I.C.G+mh2
=Mi212+mh2
=Mi212+M(0.3)2
=M(112+1.09)
=M(1+1.0812)
=M(2.0812)
T=2π(lmgl)
=2π√2ma23mgl
=2π√2a2√23ga)
=2π√8a3g
dh=r2
l=r2=Dist.betweenC.G.andsuspensionp∮<br>M.I.,aboutA, l-I_(C.G.)+Mh^2<br>(mr^2)/2+m(r/2)^2<br>=mr^2(1/2+1/4)=3/4mr^2<br>:. T=2pisqrt(I/(mgl))=2pisqrt((3mr^2)/(4mgl))<br>=2pisqrt((3r^2)/(4gr/2))=2pisqrt((3r)/(2g))
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:HC VERMAChapter:SIMPLE HARMONIC MOTIONExercise:Objective-2
Explore 2 Videos
- ROTATIONAL MECHANICSBook:HC VERMAChapter:ROTATIONAL MECHANICSExercise:Exercises
Explore 86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBook:HC VERMAChapter:SOME MECHANICAL PROPERTIES OF MATTERExercise:Exercises
Explore 32 Videos
Similar Questions
Compound pendulum are made of :
(a) A rod of length l suspended through a point located at distance l/4 from centre of rod.
(b) A ring of mass m and radius r suspended through a point on its periphery.
(c) A uniform square plate of edge a suspended through a corner.
(d) A uniform disc of mass m and radius r suspeneded through a point r/2 away from the centre.
Find the time period in each case.
View SolutionFind the time period of small oscillations of the following systems.
(a) A uniform rod of mass m and length L is suspended through a pin hole at distance L/4 from top as shown.
(b) A ring of mass m and radius r suspended through a point on its periphery.
(c) A uniform disc of mass m and radius r suspended through a point r/2 away from centre.
(d) A uniform square plate of edge a suspended through a corner.
View Solution
Knowledge Check
Find time period of uniform disc of mass m and radius r suspended through point r/2 away from centre, oscillating in a plane parallel to its plane.
A2π√2r3gB4π√r2gC2π√3r2gDNone of theseThe radius of gyration of a uniform solid sphere of radius R., about an axis passing through a point R2 away from the centre of the sphere is:
A√1320RB√2340RC√2320RD√1340RA uniform thin ring of radius R and mass m suspended in a vertical plane from a point in its circumference. Its time period of oscillation is
A2π√rgB2pi sqrt((5 R)/(3 g))C2π√7R5gD2π√2R5g
Calculate the time period of a uniform square plate of side 'a' if it is suspended through a corner.
View SolutionA disc of mass 'm' is suspended at a point R/2 above its centre. Find its period of oscillation.
View SolutionA ring of radius r is suspended from a point on its circumference. Determine its angular frequency of small oscillations.

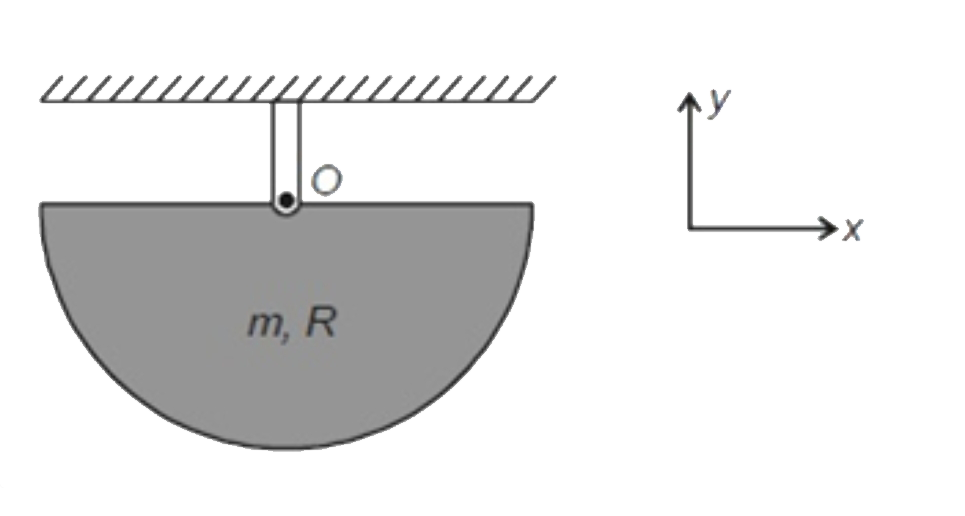
View SolutionTime period for small oscillations in vertical x - y plane of uniform semi - circular disk of mass m and radius R , about horizontal axis through point O, is equal to
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View Solution
