If three square are chosen at random on a chess Board, show that chance that they should be in a diagonal line 7/744.
7744
5744
7544
11744
The correct Answer is:A
We can choose three squares in a diagonal line parallel to BD in the ΔABD. Clearly, three squares in ΔABD and in a diagonal line parallel to BD can be chosen in

.3C3+.4C3+.5C3+.6C3+.7C3+.8C3 ways
Similarly, in ΔBCD, the squares can be chosen parallel to BD in an equal number of ways. Hence, the total number of ways in which three squares can be chosen in a diagonal line parallel to BD is
2(.3C3+.4C3+.5C3+.6C3+.7C3)+.8C3 [∵ BD is common to both the triangles]
Similarly, squares can be chosen in a diagonal line parallel to AC and hence the total number of favourable ways
=4(.3C3+.4C3+.5C3+.6C3+.7C3)+2.8C3=392
Hence, the required probability =392.64C3
=392×664.63.62=7744
Topper's Solved these Questions
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:Exercise 1 (TOPICAL PROBLEMS)
Explore 44 Videos
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:Exercise 2 (MISCELLANEOUS PROBLEMS)
Explore 40 Videos
- PROBABILITYBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PROBABILITYExercise:MHT CET Corner
Explore 4 Videos
- PRACTICE SET 24Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:PRACTICE SET 24Exercise:Paper 2 (Mathmatics)
Explore 50 Videos
- SEQUENCES AND SERIES Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:SEQUENCES AND SERIES Exercise:EXERCISE 31
Explore 1 Video
Similar Questions
The probability distribution of a random variable X is given as
Then, the value of p is

View SolutionIf a random variable X has the following probability distribution values of X
Then P(X≥6) is equal to

View SolutionIf a random variable waiting time in minutes for bus and probability density function of x is given by
f(x)={15,0≤x≤50,otherwise
Then probability of waiting time not more than 4 minutes is equal to
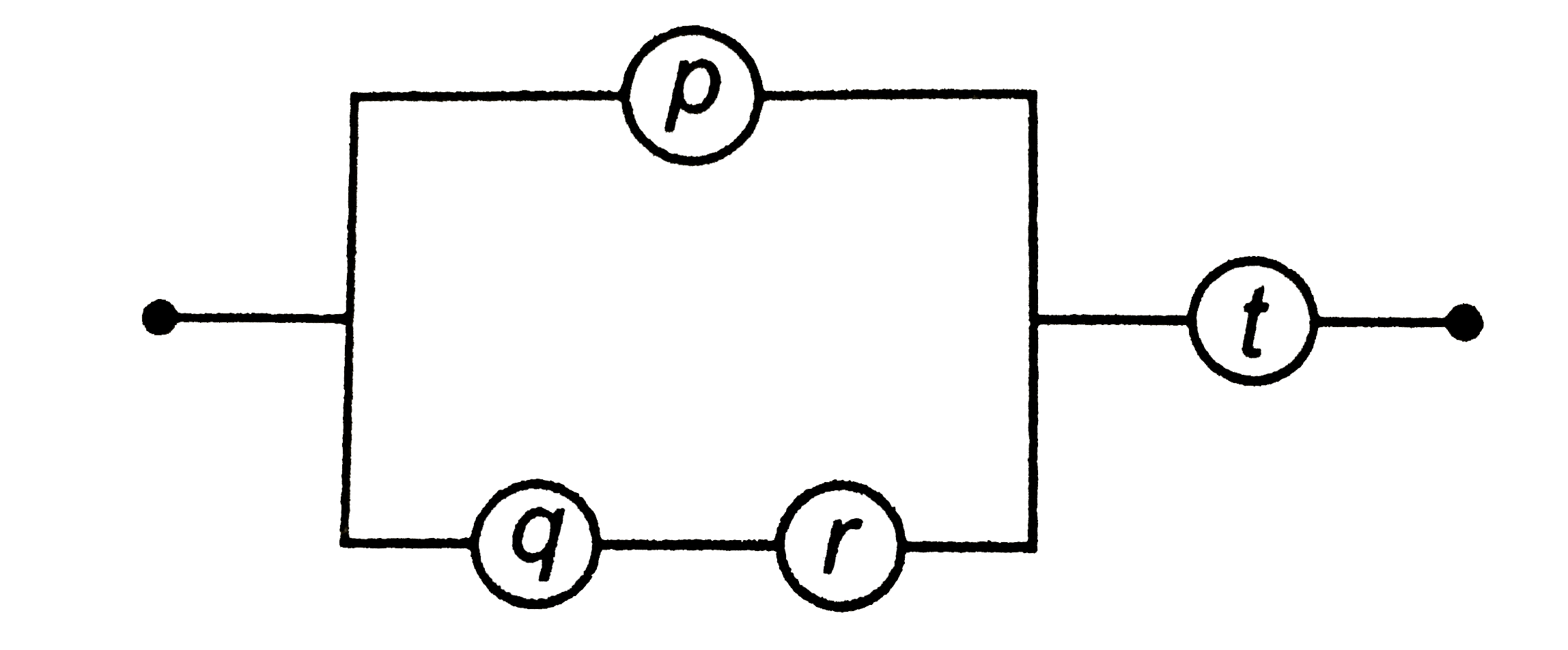
View SolutionThe switching function for the following network is
View SolutionThe coefficient of x3 in the expansion of 3x is
View SolutionIf 4 squares are chosen at random on a chess board,the probability that they lie on a diagonal line is
View SolutionIf three square are chosen at random on a chess Board,show that chance that they should be in a diagonal line 7/744.
View SolutionIf two of the 64 squares are chosen at random on a chess board, the probability that they have a side in common is
View SolutionThree '1xx1' squares of a chess board having 8xx8 squares being chosen at random,the chance that all the three are white is
View SolutionThree '1xx1 'squares of a chess board having 8xx8 squares are chosen at trandom,the chance that all the three of the same colour is
View SolutionIf nine squares are chosen at random on a chess board,find the probability that they form a square of size 3xx3 .
View SolutionOn a chess board if two squares are chosen at random, what is the probability that they haven't a side in common?
View SolutionIf four squares are chosen at random on a chess board, then the probability that they lie in a diagonal line is
View SolutionIf four squares are chosen at random on a chess board, then the probability that they lie in a diagonal line is
View SolutionIf 7 squares are chosen at random on a chess board, the probability that they lie on a diagonal line is
View SolutionTwo squares of a chess board are chosen at random, the probability that two are of one colour
View Solution
