Three charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
To find the electric field at the fourth corner of a square where three charges are placed at three corners, we can follow these steps:
Step 1: Understand the Configuration
We have three charges, each equal to q, placed at three corners of a square with side length a. We need to find the electric field at the fourth corner (let's call it point D).
Step 2: Determine the Electric Field Due to Each Charge
1. Electric Field due to Charge at Corner A (E1):
- The charge at corner A creates an electric field at point D directed away from A (since the charge is positive).
- The distance from A to D is a.
- The magnitude of the electric field E1 is given by:
E1=kqa2
- The direction of E1 is along the line AD.
2. Electric Field due to Charge at Corner B (E2):
- The charge at corner B also creates an electric field at point D directed away from B.
- The distance from B to D is a.
- The magnitude of the electric field E2 is:
E2=kqa2
- The direction of E2 is along the line BD.
3. Electric Field due to Charge at Corner C (E3):
- The charge at corner C creates an electric field at point D directed away from C.
- The distance from C to D is √2a (the diagonal of the square).
- The magnitude of the electric field E3 is:
E3=kq(√2a)2=kq2a2
- The direction of E3 is directed towards point D from point C.
Step 3: Resolve the Electric Fields into Components
- The electric fields E1 and E2 are along the axes of the square.
- The electric field E3 can be resolved into its x and y components since it is at a 45∘ angle to the axes:
E3x=E3⋅cos(45∘)=kq2a2⋅1√2=kq2√2a2
E3y=E3⋅sin(45∘)=kq2a2⋅1√2=kq2√2a2
Step 4: Calculate the Resultant Electric Field
- The total electric field in the x-direction Ex is:
Ex=E1+E3x=kqa2+kq2√2a2=kqa2(1+12√2)
- The total electric field in the y-direction Ey is:
Ey=E2+E3y=kqa2+kq2√2a2=kqa2(1+12√2)
Step 5: Calculate the Magnitude of the Resultant Electric Field
- The magnitude of the resultant electric field Enet can be calculated using the Pythagorean theorem:
Enet=√E2x+E2y=
⎷2(kqa2(1+12√2))2
Enet=kqa2(1+12√2)√2
Final Result
Thus, the electric field at the fourth corner is:
Enet=kq√2a2(1+12√2)
We have three charges, each equal to q, placed at three corners of a square with side length a. We need to find the electric field at the fourth corner (let's call it point D).
1. Electric Field due to Charge at Corner A (E1):
- The charge at corner A creates an electric field at point D directed away from A (since the charge is positive).
- The distance from A to D is a.
- The magnitude of the electric field E1 is given by:
E1=kqa2
- The direction of E1 is along the line AD.
- The charge at corner B also creates an electric field at point D directed away from B.
- The distance from B to D is a.
- The magnitude of the electric field E2 is:
E2=kqa2
- The direction of E2 is along the line BD.
- The charge at corner C creates an electric field at point D directed away from C.
- The distance from C to D is √2a (the diagonal of the square).
- The magnitude of the electric field E3 is:
E3=kq(√2a)2=kq2a2
- The direction of E3 is directed towards point D from point C.
- The electric fields E1 and E2 are along the axes of the square.
- The electric field E3 can be resolved into its x and y components since it is at a 45∘ angle to the axes:
E3x=E3⋅cos(45∘)=kq2a2⋅1√2=kq2√2a2
E3y=E3⋅sin(45∘)=kq2a2⋅1√2=kq2√2a2
- The total electric field in the x-direction Ex is:
Ex=E1+E3x=kqa2+kq2√2a2=kqa2(1+12√2)
Ey=E2+E3y=kqa2+kq2√2a2=kqa2(1+12√2)
- The magnitude of the resultant electric field Enet can be calculated using the Pythagorean theorem:
Enet=√E2x+E2y=
⎷2(kqa2(1+12√2))2
Enet=kqa2(1+12√2)√2
Thus, the electric field at the fourth corner is:
Enet=kq√2a2(1+12√2)
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBook:HC VERMAChapter:ELECTRIC FIELD AND POTENTIALExercise:Short Answer
Explore 14 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMAChapter:ELECTRIC FIELD AND POTENTIALExercise:Objective 1
Explore 9 Videos
- ELECTRIC FIELD AND POTENTIALBook:HC VERMAChapter:ELECTRIC FIELD AND POTENTIALExercise:Exercises
Explore 75 Videos
- ELECTRIC CURRENT THROUGH GASESBook:HC VERMAChapter:ELECTRIC CURRENT THROUGH GASESExercise:Exercises
Explore 23 Videos
- ELECTROMAGNETIC INDUCTIONBook:HC VERMAChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE
Explore 9 Videos
Similar Questions
The charge on a proton is +1.6X10(−19)C and that on an
. electron is −1.6X10(−19)C. Does it mean that the electron
. has a charge 3.2X10(−19)c less than the charge of a
. proton?
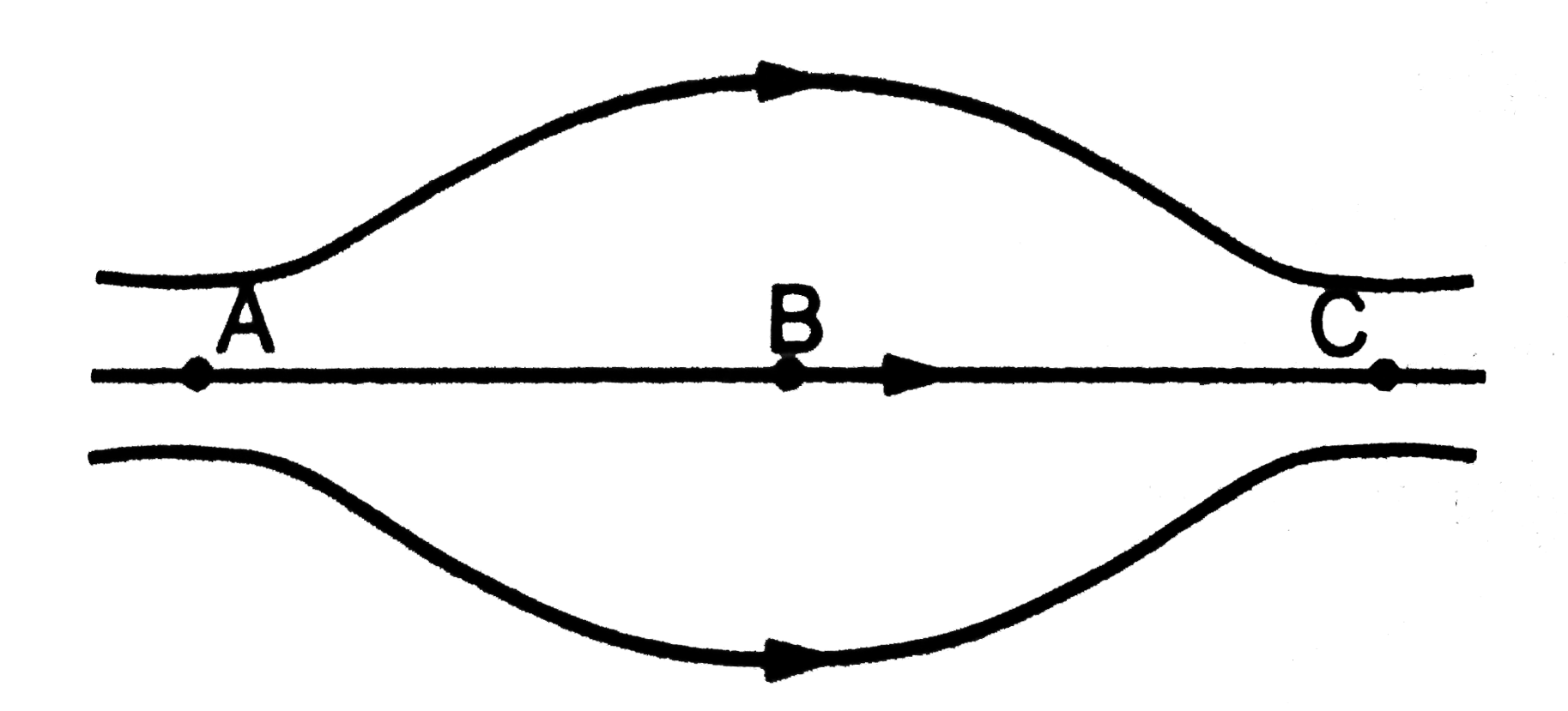
View SolutionFigure shows some of the electric field lines correspoinding to an electric field. The figure suggests that
View SolutionFind the dimensional formula of ε0 .
View SolutionA discharge tube contains helium at a low pressure. A large potential difference is applied across the tube. Consider a helium atom that has just been ionized due to the detachment of an atomic electron. Find the ratio of the distance travelled by the free electron to that by the positive ion in a short time dt after the ionization.
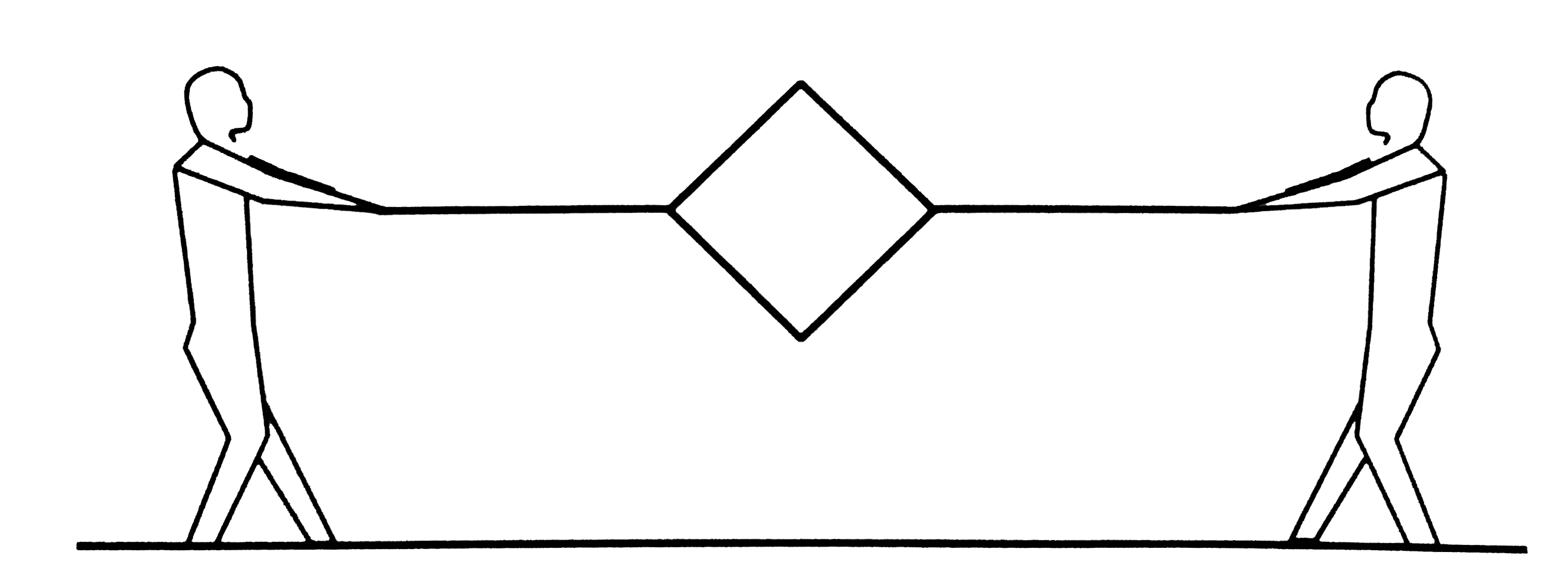
View SolutionShown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
View SolutionThree equal charges, each +q are placed on the corners of an equilatreal triangel . The electric field intensity at the centroid of the triangle is
View SolutionThree masses, each equal to M, are placed at the three corners of a square of side a. the force of attraction on unit mass at the fourth corner will be
View SolutionPoint charge of 3×10−9C are situated at each of three corners of a square whose side is 15cm. The magnitude and direction of electric field at the vacant corner of the square is
View Solutionभुजा a वाले एक वर्ग के प्रत्येक कोने पर आवेश q रखा है। वर्ग के केन्द्र पर परिणामी विद्युत् क्षेत्र की गणना कीजिए।
View SolutionThree charges each equal to +4nC are placed at the three comers of a square of side 2 cm. Find the electric field at the fourth corner.
View Solutiona भुजा वाले वर्ग के तीन कोनों पर तीन आवेश (हर एक की मात्रा q) रखे जाते हैं। चौथे कोने पर वैद्युत क्षेत्र ज्ञात करें।
View SolutionThree charges each equal to +4nC are placed at the three comers of a square of side 2 cm. Find the electric field at the fourth corner.
View SolutionThree bodies each of mass.m. are placed at the three corners of a square of side .a.. The gravitational force on unit mass kept at the fourth corner is:
View SolutionThree bodies each of mass 'm' are placed at the three corners of a square of side 'a'. The gravitational force on unit mass kept at the fourth corner is
View SolutionThree bodies each of mass 'm' are placed at the three corners of a square of side 'a'. The gravitational force on unit mass kept at the fourth corner is
View SolutionThree masses, each equal to M, are placed at the three corners of a square of side a. the force of attraction on unit mass at the fourth corner will be
View Solution
