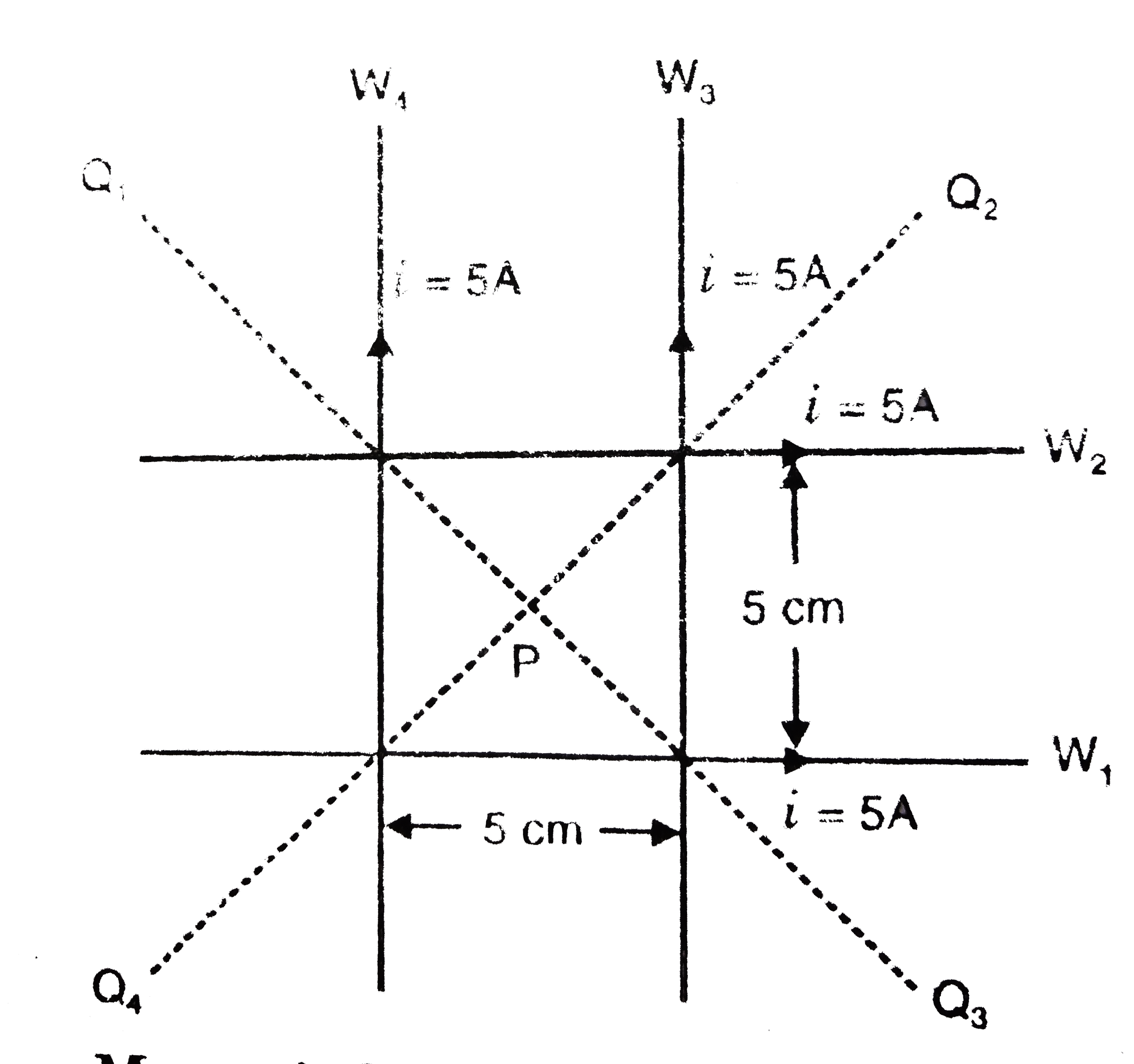
Four long, straight wires, each carrying a current of 5.0 A, are placed in a plane as shown in figure . The points of intersection form a square of side 5.0 cm. (a) Find the magnetic field at the centre P of the square. (b) Q1,Q2,Q3andQ4 are points situated on the diagonals of the square and at a distance from P that is equal to the length of the diagonal of the square. Find the magnetic fields at these points.

Magnetic field at P due to wire W1 and W2 = 0 Magnetic field at P due to wires W3 and W4 = 0 Hence net magnetic field at P due to these four wires = 0 (b) At point Q1 Magneticfield due to W1=4×10−5T along? Magnetic field due to W2=43×10−5T along? Magneticj field due to W3=4×10−5Talong? Magnetic field due to W4=43×10−5T along? So net B at Q1=((4+43+4+43)×10−5T =323×106(−5)T =1.06×10−4T along 3 At point Q2 Magnetic field due to wire W1=4×10−5T along oxMag≠ticfielddue→wireW_2 = (4)/(3) xx10^(-5) T along oxMag≠ticfielddue→wireW_3 = (4)/(3) xx10^(-5)T along oxMag≠ticfielddue→wireW_4 = 4xx10^(-5)T along ox
Hence≠tB=0Similarlyatp∮Q_3andQ_4mag≠ticfieldbe1.1×10−4Talongox and zero.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMACHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMACHAPTER - MAGNETIC FIELDEXERCISE - Exercises
61 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Exercises
9 Videos
Similar Questions
Four long wires each carrying current I as shown in the figure are placed at the points A, B, C and D. Find the magnitude and direction of
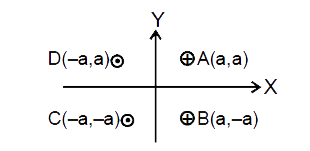
magnetic field at the centre of the square.
View SolutionTwo long wires a and b, carrying equal currents of 10*0A, are placed parallel to each other with a separation of 4*00 cm between them as shown in figure. Find the magnetic field B at each of the points P,Q and R.

View Solution
Knowledge Check
Four long wires each carrying current I as shown in Fig. are placed at points A, B, C and D. Find the magnitude and direction of

magnetic field at the centre of the square.Aμ04π(Ia) along Y-axisBμ04π(4Ia) along X-axisCμ04π(4Ia) along Y-axisDNone of theseThe magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current I is :
Aμ0LπLBμ0LπLC√2μ0LπLD2√2μ0LπLThe magnetic field at the point of intersection of diagonals of a square loop of side L carrying a current I is :
Aμ0LπLBμ0LπLC√2μ0LπLD2√2μ0LπL
Four charges +q,+2q,+3q and +4q are placed at the four corners ABCD of a square of side a. Calculate the field and potential at the centre of the square.
View SolutionFour very long, current carrying wires in the same plane intersect to form a square 40.0cm on each side as shown in figure. Find the magnitude and direction of the current I so that the magnetic field at the centre of square is zero. Wires are insulated from each other.

View SolutionA current carrying wire is in form of square loop of side length 10 cm. current in wire is 5A. Find out magnetic field at centre of loop.
View SolutionP, q and R are long straight wires in air, carrying currents as shown in the figure. The force on Ois directed

View SolutionCharges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along

View Solution

