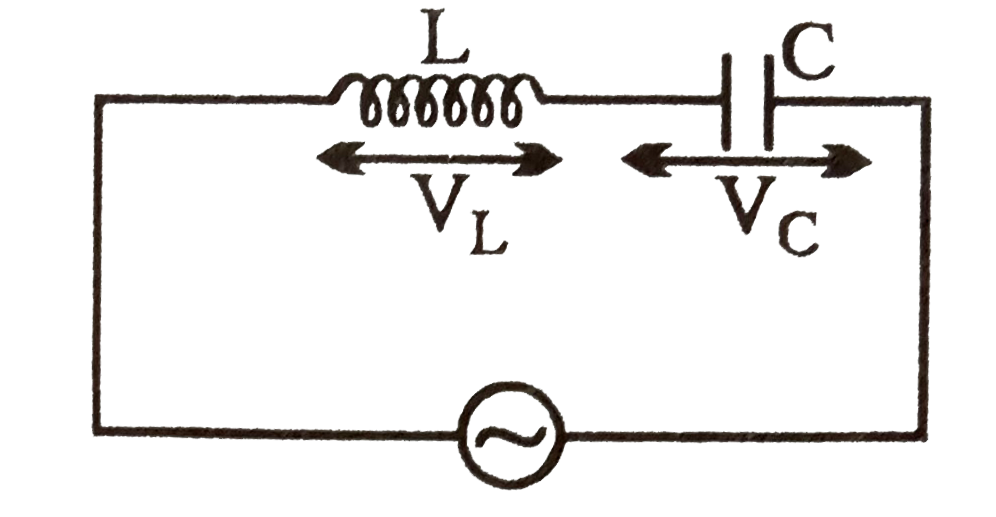
In a series LCR circuit with an AC source, R=300Ω,C=20μF,L=1.0henry,εrms=50V and v=50πHz. Find (a) the rms current in the circuit and (b) the rms potential differences across the capacitor, the resistor and the inductor. Note that the sum of the rms potential differences across the three elements is greater than the rms voltage of the source.
Given R=300Ω, C=20μF
=(20×10−6)F,
L=1Henry,
E=50V, v=50/πHz
(a) i0=E0z
and Z=√R2+(Xe−XL)2
=√(300)2+(1/2πfC−2πfL)2
=
⎷(300)2+(12π×50/π×20×10−6−2π×50π×1)2
=
⎷(300)2+(10420−100)2=500
:. i0=E0Z=50500=0.1A
(b) Potential across the capacitor
=i0×XC=0.1×500=50V
Potential difference across the resistor
=i0×R=0.1×300=30V
Potential difference across the inductor
=i0×XL=0.1×100
=10V
R.M.S. potential =50V
Net sum of all the potential drops
=50V+30V+10V
=90V
Sum of potential drops = R.m.s potential applied.
Topper's Solved these Questions
Similar Questions
In a series RC circuit with an AC source, R=300Ω,C=25μF,ε050V and v=50(Π)Hz. Find the peak current and the average power dissipated in the circuit.
View SolutionIn a series LCR circuit with an AC source of effective voltage 50 V , frequency ν=50/π Hz R= 300ΩC=20μF and L = 1.0 H. Find the rms current in the circuit.
View Solution
Knowledge Check
In the circuit shown, rms circuit is 11 A . The potential difference across the inductor is
 A220 VB0 VC300 VD200 V
A220 VB0 VC300 VD200 VAn alternating e.m.f. of 100V (rms) is applied to a series LCR circuit. At resonance, the potential difference across the inductance and across the capacitance is 400V each. The potential difference across the resistance will be
A100VB400VC800VDzeroThe current I, potential difference VL across the inductor and potential difference VC across the capacitor in circuit as shown in the figure are best represented vectorially as
 A
A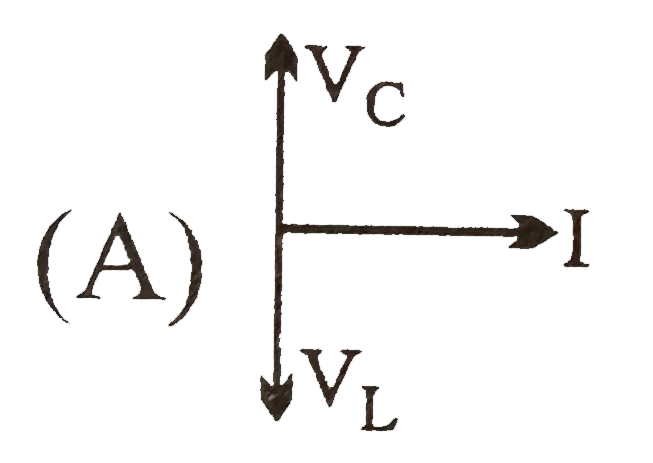 B
B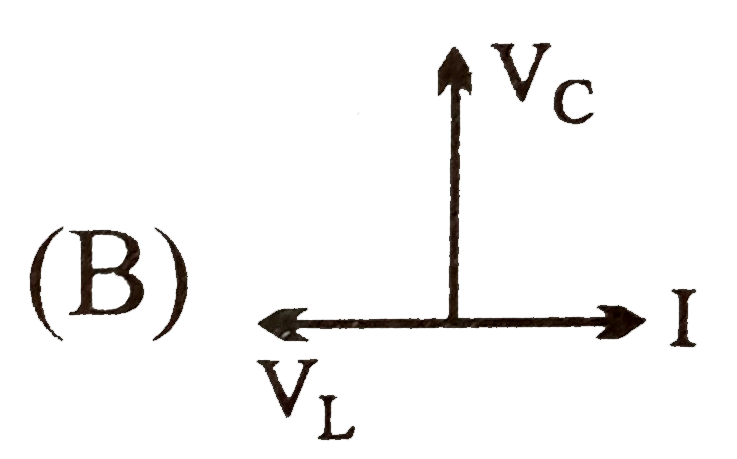 C
C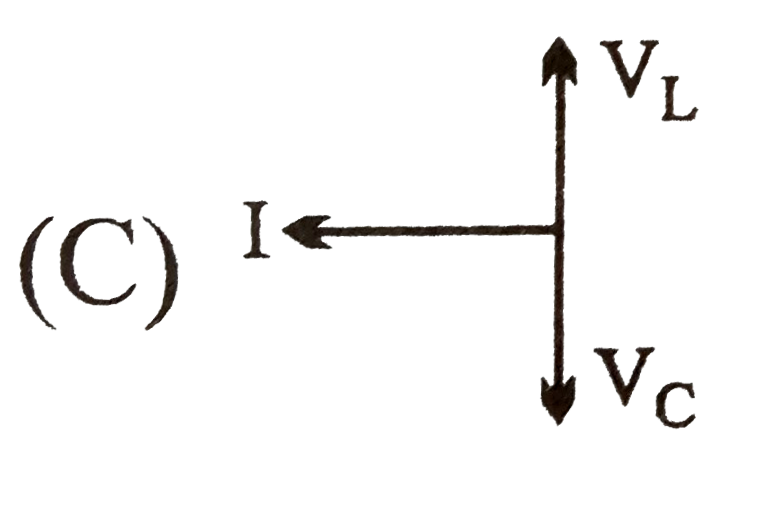 D
D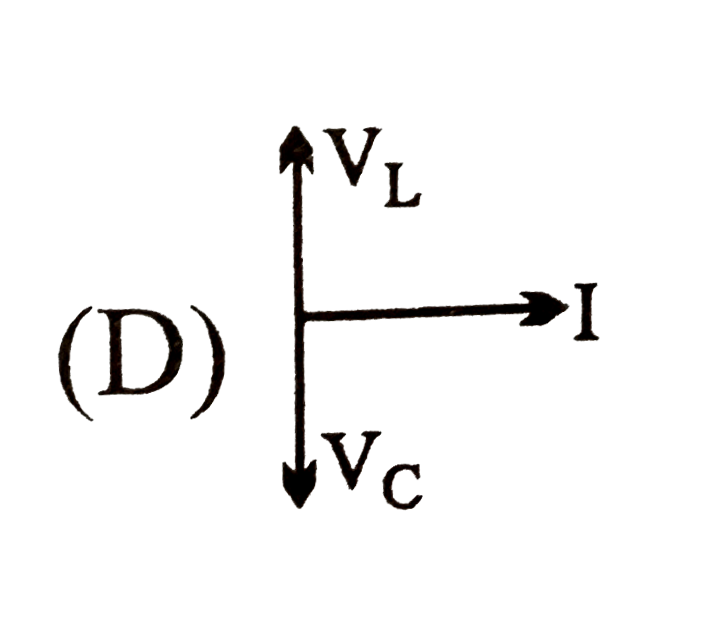
(a) In a series L-C-R circuit with an AC source, R =300Ω, C = 20μF,L=1.0H,V0=50√2Vandf=50πHz. Find (i) the rms current in the circuit and (ii) the rms voltage across each element.
(b) Consider the situatiuon of the previous part. find the average electric field energy stored in the capacitor and the average magnetic field energy stored iun the coil .
View SolutionFigure here, shows a series L-C-R circuit connected to a variable frequency 230 V source. L = 5.0H, C = 80μF and r =40Ω
(a) Determine the source frequency which drives the circuit in resonance.
(b) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency.
(c) Determine the rms potential drops across the three elements of the circuit. show that the potential drop across the L-C combination is zero at the resonating frequency.

View SolutionTwo resistors are connected in series across 5V rms source of alternating potentail. The potential difference across 6Ω resistor is 3Vm. If R is replaced by a pure inductor L of such magnitude that current remains same, then the potential difference across L is
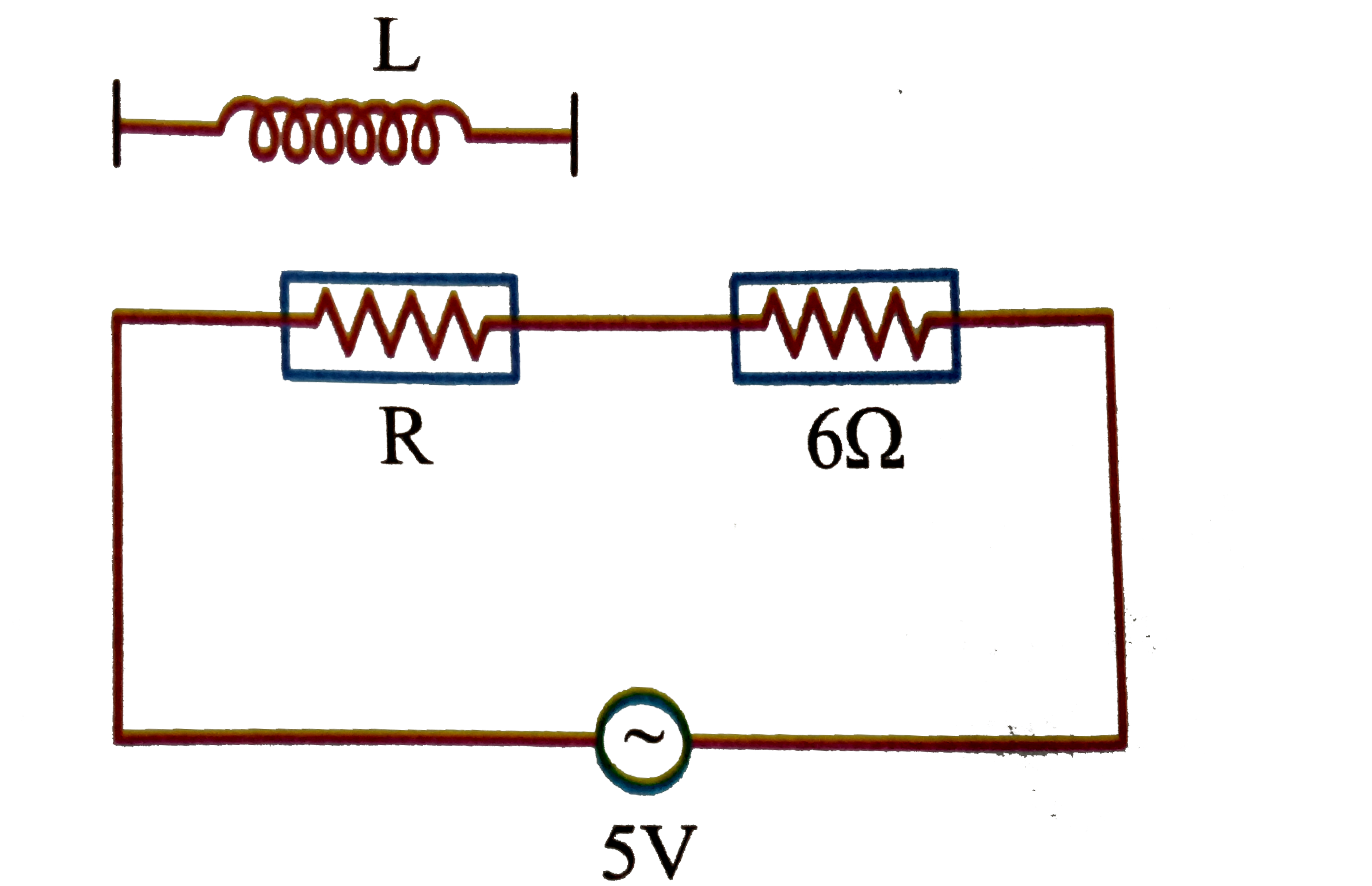
View SolutionIn a series LCR circuit with an AC source (Erms50Vandv=50/πHz),R=300Ω,C=0.02mF,L=1.0H , which of the following is correct
View SolutionTwo resistor are connected in series across a 5 V rms source of alternating potential. The potential difference across 6Ω resistor is 3V. If R is replaced by a pure inductor L of such magnitude that current remains same. Then the potential difference across L is

View Solution
