At constant temperature, the equilibrium constant (Kp) for the decomposition reaction N2O4(g)⇔2NO2(g) is expressed by Kp=4x21−x2P, where P = pressure, x = extent of decomposition. Which one of the following statements is true?
Kp remains constant with change in P and x
Kp increases with increase of P
Kp increases with decrease of x.
Kp increases with increase of x.
The correct Answer is:A
Kp can be written as:
Kp=4x21−x2P
With change of pressure, x will change in such a way that Kp remains a constant at a particular temperature.
Topper's Solved these Questions
- EQUILIBRIUM TEST (CHEMICAL)-1BOOK - NTA MOCK TESTSCHAPTER - EQUILIBRIUM TEST (CHEMICAL)-1EXERCISE - SINGLE CHOICE
30 Videos
- ENVIRONMENTAL CHEMISTRY TESTBOOK - NTA MOCK TESTSCHAPTER - ENVIRONMENTAL CHEMISTRY TESTEXERCISE - CHEMISTRY
30 Videos
- GENERAL ORGANIC CHEMISTRY TEST-1BOOK - NTA MOCK TESTSCHAPTER - GENERAL ORGANIC CHEMISTRY TEST-1EXERCISE - MULTIPLE CHOICE QUESTIONS
30 Videos
Similar Questions
Bromine monochloride ( BrCl ) decomposes into bromine and chlorine according to reaction 2BrCl(g)=Br2(g)+Cl2(g),Kc=32 at 500 K. If initially, pure BrCl is taken at concentration 3.3×10−3mol L−1, what is its molar concentration in the mixture at equilibrium state?
View SolutionEutrophication causes reduction in
View SolutionThe correct IUPAC name of the following hydrocarbon is
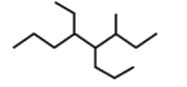
View SolutionAt constant temperature, the equilibrium constant (Kp) for the decomposition reaction
N2O4⇔2NO2
is expressed by Kp=4x2p/(1−x2), where p=pressure x= extent of decomposition. Which of the following statements is true?
View SolutionAt constant temperature, the equilibrium constant (Kp) for the decomopsition reaction N2O4⇔2NO2 is expressed by Kp=(4x2P)(1−x2), where P = pressure, x = extent of decomposition. Which one of the following statement is true ?
View SolutionAt constant temperature, the equilibrium constant Kp for by Kp=4x2p(1−x2), where p= pressure x= extent of decomposition. Which one of the following statement is true?
View SolutionAt constant temperature, the equilibrium constant (Kp) for the decomopsition reaction N2O4⇔2NO2 is expressed by Kp=(4x2P)(1−x2), where P = pressure, x = extent of decomposition. Which one of the following statement is true ?
View SolutionAT constant temperature, the equilibrium constant (Kp) for the decomposition reaction
N2O4⇔2NO2 is expressed by Kp=(4x2P)/(1−x2), where P= pressure ,x = extent of decomposition . Which one of the following statements is true ?
View SolutionAt constant temperature, the equilibrium constant (Kp) for the decomposition reaction, N2O4⇔2NO is expressed by Kp=(4x2P)(1−x2), where P = pressure, x = extent of decomposition. Which one of the following statements is true?
View SolutionAt constant temperature, the equilibrium constant (Kp) for the decomposition reaction N2O4⇔2NO2 is expressed by Kp=4x2P/(1−x2) where Pis pressure, x is extent of decomposition. Which of the following statement is true ?
View Solutionवियोजन अभिक्रिया, N2O4↔2NO2 के लिए स्थिर तापक्रम पर साम्य स्थिरांक (Kp)कामाननिम्नव्यंजकद्वारादियाजाताहै<br>K_(p)=((4x^(2).p))/((1-x^(2)))
जहाँ, p = दाब, - वियोजन की मात्रा
निम्न में से कौन-सा कथन सत्य है?
View SolutionFor the equilibrium N2O4(g)⇔2NO2(g), the KpandKc values are related as
View SolutionFor the equilibrium N2O4(g)⇔2NO2(g), the KpandKc values are related as
View SolutionAt constant temperature, the equilibrium constant (K_p) for the decomposition reaction, N_2O_4 hArr 2NO_2 is expressed by K_p=4x^2P//(1-x^2) , where P = pressure and x = extent of decomposition. Which of the following statements is true?
View SolutionAt constant temperature, the equilibrium constant (Kp) for the decomposition reaction .
N2O4⇔2NO2, is expressed by Kp=4x2P1−x2 where P = pressure, x = extent of decomposition. Which one of the following statements are false ?
View SolutionAt constant temperature, the equilibrium constant (K_(P)) for the decomposition reaction. N _(2)O_(4) hArr 2NO _(2) is expressed by K _(P) = 4x ^(2) P //(1 - x ^(2)) where, P is pressure, x is extent of decomposition. Which of the following statement is true?
View Solution

