For a given value of 'l' the total number of 'm' values is ____________
The correct Answer is:2l+1
To solve the question "For a given value of 'l' the total number of 'm' values is ____________", we need to understand the relationship between the azimuthal quantum number (l) and the magnetic quantum number (m).
1. Understanding Quantum Numbers:
- Quantum numbers are values that describe the unique quantum state of an electron in an atom. The main quantum numbers are:
- Principal quantum number (n)
- Azimuthal quantum number (l)
- Magnetic quantum number (m)
- Spin quantum number (s)
2. Defining the Azimuthal Quantum Number (l):
- The azimuthal quantum number (l) determines the shape of the orbital and can take on integer values from 0 to (n-1), where n is the principal quantum number.
3. Understanding the Magnetic Quantum Number (m):
- The magnetic quantum number (m) describes the orientation of the orbital in space. For a given value of l, the possible values of m range from -l to +l.
4. Calculating the Total Number of m Values:
- The total number of possible m values for a given l can be calculated using the formula:
Total m values=2l+1
- This formula accounts for all integer values from -l to +l, including zero.
5. Examples:
- If l = 0 (s orbital):
- m can be 0 → Total m values = 2(0) + 1 = 1
- If l = 1 (p orbital):
- m can be -1, 0, +1 → Total m values = 2(1) + 1 = 3
- If l = 2 (d orbital):
- m can be -2, -1, 0, +1, +2 → Total m values = 2(2) + 1 = 5
- If l = 3 (f orbital):
- m can be -3, -2, -1, 0, +1, +2, +3 → Total m values = 2(3) + 1 = 7
Final Answer:
For a given value of 'l', the total number of 'm' values is 2l + 1.
- Quantum numbers are values that describe the unique quantum state of an electron in an atom. The main quantum numbers are:
- Principal quantum number (n)
- Azimuthal quantum number (l)
- Magnetic quantum number (m)
- Spin quantum number (s)
- The azimuthal quantum number (l) determines the shape of the orbital and can take on integer values from 0 to (n-1), where n is the principal quantum number.
- The magnetic quantum number (m) describes the orientation of the orbital in space. For a given value of l, the possible values of m range from -l to +l.
- The total number of possible m values for a given l can be calculated using the formula:
Total m values=2l+1
- This formula accounts for all integer values from -l to +l, including zero.
- If l = 0 (s orbital):
- m can be 0 → Total m values = 2(0) + 1 = 1
- If l = 1 (p orbital):
- m can be -1, 0, +1 → Total m values = 2(1) + 1 = 3
- If l = 2 (d orbital):
- m can be -2, -1, 0, +1, +2 → Total m values = 2(2) + 1 = 5
- If l = 3 (f orbital):
- m can be -3, -2, -1, 0, +1, +2, +3 → Total m values = 2(3) + 1 = 7
For a given value of 'l', the total number of 'm' values is 2l + 1.
Similar Questions
Knowledge Check
The total number of m values for n=4 is
A8B16C12D20For a given value of quantum number l , the number of allowed values of m is given by
Al+2B2l+2C2l+1Dl+1For the azimuthal quantum number 'I' the total number of magnetic quantum numbers is given by
Al=m+12Bl=m−12Cl=2m+12Dm=2l+12
Set A has m element and Set B has n element . If the total numbers of subsets of A is 112 more than the total number of subsets of B, then the value of m.n is _____________
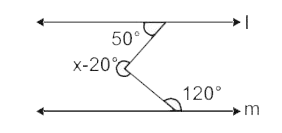
View SolutionFor what value of x , l||m.
View SolutionTwo finite sets have m and 3 elements respectively. The total number of subsets of first set is 56 more than the total number of subsets of the second set. The value of m is ___________
View SolutionIn the given figure, if l∣∣m, then the value of x∘=
View SolutionAn electron is in a state with n=4. What are (a) the number of possible values of l, (b) the number of possible values of ml, (c ) the number of poosible values of ms, (d) the number of states in the n=4 shell, and (e) the number of subshells in the n=4 shell?
View Solution

